제 29회 전국 대학생 수학 경시대회 제 1 분야
추천글 : 【전국 대학생 수학경시대회】 전국 대학생 수학경시대회 풀이 모음
제 29회 전국 대학생 수학 경시대회
제 1 분야
2010년 10월 2일 (10:00 - 13:00)
1. 연속함수 f가 f(x) + f(x + 1) + … + f(x + 2009) = x2009을 만족할 때, 다음 적분값을 구하여라.

Solution.

2. 행렬 A의 최소다항식을 구하고, B2 = A인 행렬 B가 존재하지 않음을 보여라.

Solution.

3. f(x) = xm + am-1xm-1 + am-2xm-2 + … + a1x + a0가 xn-1을 나누고,
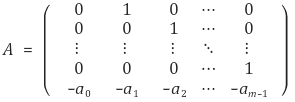
일 때,
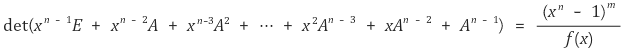
임을 보여라. (단, 행렬 E는 m차 단위행렬이다.)
Solution.

4. p가 소수이고 p - 1은 7의 배수가 아닐 때, n7 - 2010이 p의 배수가 되는 자연수 n이 무수히 많음을 보여라.
Solution.

5. 적분
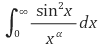
가 수렴하는 실수 α의 값을 모두 구하여라.
Solution.
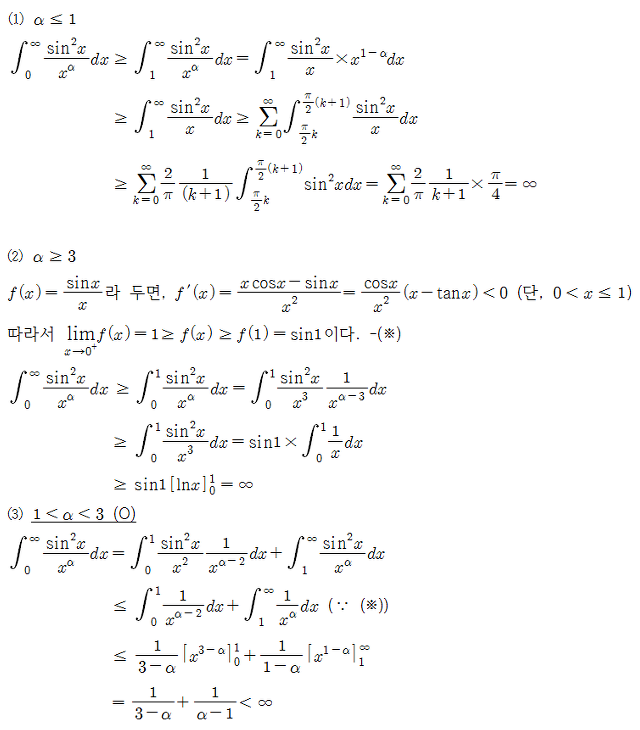
6. 함수 f : ℝ → ℝ의 도함수 f '이 ℝ에서 연속이다. x ≠ y일 때, g(x, y) = ( f(x) - f(y) ) / (x - y)라 하면, g가 ℝ2에서 연속이 되도록 g(x, x)를 정의할 수 있음을 보여라.
Solution.
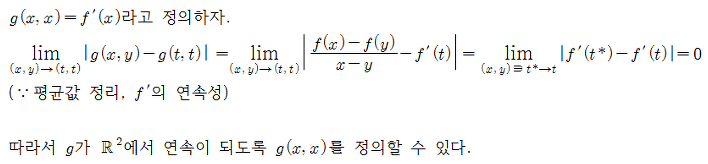
7. 다음 적분값을 구하여라.
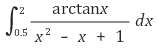
Solution.

8. 다음 식을 만족하는 두 양수 a와 r을 구하여라.
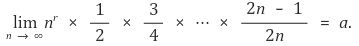
Solution.

입력: 2015.09.28 21:02
'▶ 자연과학 > ▷ 전국 대학생 수학경시대회' 카테고리의 다른 글
| 【대수경】 제 28회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2016.06.26 |
|---|---|
| 【대수경】 제 29회 전국 대학생 수학 경시대회 제 2 분야 (0) | 2016.06.26 |
| 【대수경】 제 30회 전국 대학생 수학 경시대회 제 2 분야 (2) | 2016.06.25 |
| 제 30회 전국 대학생 수학 경시대회 제 1 분야 #08 (0) | 2016.06.25 |
| 【대수경】 제 30회 전국 대학생 수학 경시대회 제 1 분야 (0) | 2016.06.25 |




최근댓글