대수학 기초 문제 [21~40]
추천글 : 【수학】 수학 목차
문제 21. 아래의 주어진 저울이 모두 평형을 이룬다. ‘?’에 ⓐ만 놓을 때, ‘?’에 놓여야 할 ⓐ는 몇 개인가?
ⓐ + ⓐ + ⓑ + ⓒ = ⓐ + ⓐ + ⓐ + ⓐ + ⓑ
ⓑ + ⓑ + ⓑ + ⓑ = ⓐ + ⓐ + ⓒ + ⓒ
ⓑ + ⓑ + ⓒ = ?
풀이 21.
○ 첫 번째 식 : ⓒ = 2ⓐ
○ 두 번째 식 : 4ⓑ = 2ⓐ + 2ⓒ = 6ⓐ ⇔ 2ⓑ = 3ⓐ
○ ∴ ⓑ + ⓑ + ⓒ = 3ⓐ + 2ⓐ = 5ⓐ → 5개
문제 22. 무게가 다른 ⓐ, ⓑ, ⓒ, ⓓ 4가지 종류의 추가 있다. 천칭에 다음과 같이 추를 올려놓았을 때, 수평을 이루었다면 ⓐ는 ⓑ의 무게의 몇 배인지 구하여라.
ⓐ + ⓑ = ⓒ
ⓐ = ⓑ + ⓓ
ⓒ + ⓒ = ⓓ + ⓓ + ⓓ
풀이 22.
○ ⓒ = 1.5 ⓓ (∵ 3번째 식)
○ ⓐ + ⓑ = 2ⓑ + ⓓ = ⓒ = 1.5 ⓓ
○ ∴ ⓑ = 1/4 ⓓ
○ ∴ ⓐ = 1.5 ⓓ - ⓑ = 5/4 ⓓ
○ ∴ ⓐ는 ⓑ의 5배
문제 23. 희준, 재원, 철현이는 두 명씩 저울에 올라갔다. 희준이와 재원이가 올라갔을 때는 130 kg, 재원이와 철현이가 올라갔을 때는 127 kg, 철현이와 희준이가 올라갔을 때는 123 kg이었다. 세 명 중 가장 무거운 사람은 누구인가?
풀이 23.
○ 희준 + 재원 = 130
○ 재원 + 철현 = 127
○ 철현 + 희준 = 123
○ 2 × (희준 + 재원 + 철현) = 130 + 127 + 123 = 380 → 희준 + 재원 + 철현 = 190
○ ∴ 희준 = 63, 재원 = 67, 철현 = 60
○ 세 명 중 가장 무거운 사람 : 재원
문제 24. 동현이는 한 개에 500원짜리 큰 구슬과 한 개에 250원짜리 작은 구슬을 합하여 12개를 사려고 한다. 동현이가 가지고 있는 돈은 4800원이고, 큰 구슬을 가능한 많이 사려고 한다. 이때, 동현이가 살 수 있는 큰 구슬과 작은 구슬의 개수는 각각 몇 개인가?
풀이 24.
○ 큰 구슬의 개수를 x, 작은 구슬의 개수를 y라고 하자.
○ 조건 1. x + y = 12
○ 조건 2. 500x + 250y ≤ 4800
○ 조건 3. x, y는 음이 아닌 정수
○ (x, y) = (12, 0), (11, 1), (10, 2), ∙∙∙를 하나하나 위 조건에 대입하면 (x, y) = (7, 5)에서 지출액 4750원으로 조건에 부합함
문제 25. 80가구가 사는 어느 아파트를 조사해 보니 자녀가 없는 가구가 38가구, 딸만 있는 가구가 10가구, 그리고 아들만 있는 가구가 25가구였다. 딸, 아들 모두가 있는 가구는 몇 가구인가?
풀이 25.
○ 80 - 38 - 10 - 25 = 7가구
문제 26. 진호네 반 학생은 모두 43명이다. 이 중에서 체육을 좋아하는 학생은 28명이고, 음악을 좋아하는 학생은 19명이다. 이때, 체육과 음악 모두를 좋아하는 학생은 최소 몇 명에서 최대 몇 명까지인지 구하여라.
풀이 26.
○ 포함배제의 원리를 이용하여야 함
○ 28 + 19 - 체육과 음악 모두를 좋아하는 학생 수 = 43
○ ∴ 체육과 음악 모두를 좋아하는 학생 수 = 4
문제 27. 1과 28분의 5와 4와 20분의 19에 곱하여 자연수가 되게 하는 분수 중에서 가장 작은 분수를 구하여라.
풀이 27.
○ 1과 28분의 5 = 33 / 28
○ 4와 20분의 19 = 99 / 20
○ 결국 28과 20의 최소 공배수가 분자이고, 33과 99의 최대 공약수가 분모인 분수를 구해야 하므로 답은 140 / 33
문제 28. 축적이 1/20000인 지도에서 둘레가 50 cm인 호수가 있다. 이 호수의 둘레를 A, B 두 사람이 같은 지점에서 서로 반대쪽으로 A는 시속 5 km의 속도로, B는 시속 3 km의 속도로 동시에 출발하였다. 두 사람이 출발 후 몇 시간 몇 분만에 다시 만나게 되는지 구하여라.
풀이 28.
○ 호수의 둘레 = 50 cm × 20000 = 10 km
○ A와 B가 가까워지는 속도 = 8 km/h
○ 두 사람이 출발 후 만나는 시간 = 10 / 8 h = 1시간 15분
문제 29. 축척이 1 : 5000000인 지도에서 두 지역 사이의 직선 거리가 30 cm로 나타난 곳을 초속 500 m의 비행기로 간다면, 몇 분만에 가는지 구하여라.
풀이 29.
○ 두 지역 사이의 직선 거리 = 30 cm × 5000000 = 1500000 m
○ 비행기가 도달하는 시간 = 1500000 m / 500 m/s = 3000 s = 50 분
문제 30. 다음과 같은 규칙으로 수를 늘어놓았을 때, 100번째 수를 구하여라.
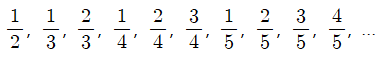
풀이 30.
○ 분모가 2, 3, 4, ∙∙∙인 분수가 1번, 2번, 3번, ∙∙∙만큼 반복하고 있음
○ 1 + 2 + ∙∙∙ + 13 = 91임을 이용
○ 즉, 92번째 분수는 1/15이고 1/15 ('92), 2/15 ('93), 3/15 ('94), 4/15 ('95), 5/15 ('96), 6/15 ('97), 7/15 ('98), 8/15 ('99), 9/15 ('100), ∙∙∙임을 이용하면 100번째 수는 9/15
문제 31. 다음과 같이 분수가 일정한 규칙에 따라 나열되어 있다. 38번째 분수와 53번째 분수의 합을 구하여라.
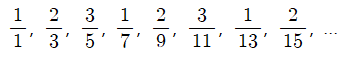
풀이 31.
○ n번째 분수의 분모는 2n-1이므로, 38번째 분수의 분모는 75, 53번째 분수의 분모는 105
○ n번째 분수의 분자는 n을 3으로 나눈 나머지이므로, 38번째 분수의 분자는 2, 53번째 분수의 분자는 2
○ 38번째 분수 + 53번째 분수 = 2 / 75 + 2 / 105 = 8 / 175 (ref)
문제 32. 다음은 ⓐ, ⓑ, ⓒ, ⓓ의 네 가지 추를 이용하여 저울 양쪽의 무게를 같게 한 것이다. 이때, ⓐ의 무게는 ⓑ의 무게의 몇 배와 같은지 구하여라.
ⓐ = ⓑ + ⓑ + ⓒ
ⓐ + ⓑ + ⓑ = ⓒ + ⓓ
ⓒ = ⓑ + ⓑ + ⓑ + ⓓ
풀이 32.
○ ⓐ + 2ⓑ = 2ⓑ + ⓒ + 2ⓑ = ⓒ + 4ⓑ = ⓒ + ⓓ
○ ∴ ⓓ = 4ⓑ
○ ⓒ = 3ⓑ + ⓓ = 3ⓑ + 4ⓑ = 7ⓑ
○ ∴ ⓐ = 2ⓑ + ⓒ = 2ⓑ + 7ⓑ = 9ⓑ
○ ∴ ⓐ의 무게는 ⓑ의 무게의 9배
문제 33. 저울에 무게가 같은 붉은 구슬 20개를 왼쪽에, 흰 구슬 6개를 오른쪽 접시에 얹었다. 오른쪽이 무거워서 흰 구슬 2개를 왼쪽으로 옮겼더니 이번에는 왼쪽이 무거워져서, 다시 왼쪽 붉은 구슬 5개를 오른쪽으로 옮겼더니 평형을 이루었다. 붉은 구슬과 흰 구슬의 총 무게는 750 g이다. 붉은 구슬과 흰 구슬의 무게를 각각 구하여라.
풀이 33.
○ 붉은 구슬 1개의 무게 = r, 흰 구슬 1개의 무게 = w
○ 식 1. 15r + 2w = 4w + 5r
○ 식 2. 20r + 6w = 750
○ ∴ r = 15, w = 75 (ref)
문제 34. 다음과 같이 분수가 규칙적으로 나열되어 있다. 6/19는 몇 번째 분수인지 구하여라.
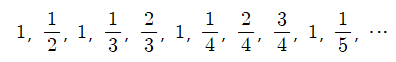
풀이 34.
○ 위 수열은 1, 1/2, 2/2, 1/3, 2/3, 3/3, 1/4, 2/4, 3/4, 4/4, 1/5, ∙∙∙와 같음을 확인
○ 분모가 1, 2, 3, ∙∙∙인 분수는 총 1번, 2번, 3번, ∙∙∙ 반복하여 나타남
○ 분모가 1 ~ 18인 분수의 총 개수는 1 + 2 + ∙∙∙ + 18 = 171개
○ {1/19, 2/19, 3/19, 4/19, 5/19, 6/19}는 원소가 6개이므로 6/19는 171 + 6 = 177번째 분수
문제 35. 작은 물통에 5컵의 물을 부어 그 무게를 달아보니 2000 g이었다. 물을 모두 비우고 같은 컵으로 8컵의 물을 부은 후 그 무게를 달아보니 2.6 kg이었다. 이 물통의 무게는 몇 g인가?
풀이 35.
○ 물통의 무게 = x, 1컵의 물의 무게 = y
○ 식 1. x + 5y = 2000
○ 식 2. x + 8y = 2600
○ ∴ x = 1000 (g), y = 200 (g)
입력: 2022.05.20 11:12
수정: 2023.08.26 11:30
'▶ 자연과학 > ▷ 대수학' 카테고리의 다른 글
| 【선형대수학】 5강. 선형대수학과 미적분 (0) | 2024.12.05 |
|---|---|
| 【수능】 2024년도 수능 수학 22번 풀이 (1) | 2023.11.21 |
| 【대수학】 대수학 기초 문제 [01~20] (2) | 2023.08.22 |
| 【선형대수학】 4강. 고유치와 고유형식 (0) | 2020.05.19 |
| 【선형대수학】 3강. 행렬식과 역행렬 (0) | 2020.04.07 |



최근댓글