5강. 선형대수학과 미적분
추천글 : 【선형대수학】 선형대수학 목차, 【해석학】 해석학 목차
1. 다변량함수의 미분 [본문]
2. 미분방정식과 고유치 [본문]
⑴ 다변수함수의 미분의 정의

⑵ 야코비 행렬(Jacobian matrix) : 영역 Ω ⊂ ℝn에서 정의된 함수 F = (f1, ···, fm)' : Ω → ℝm가 점 p ∈ Ω에서 미분가능하다고 했을 때 야코비 행렬을 다음과 같이 정의함

① 야코비 행렬을 이용한 다변수함수의 미분의 연쇄법칙

② 야코비 행렬을 이용한 다변수함수의 역함수 정리

③ 야코비 행렬을 이용한 다변수함수의 음함수 정리
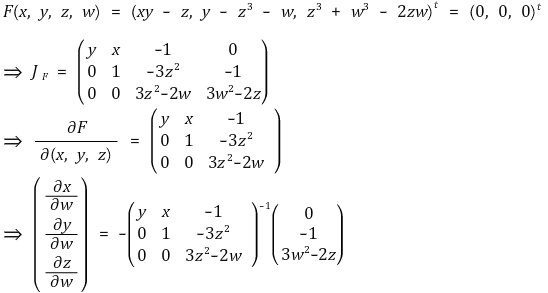
⑶ 헤세 행렬(Hessian matrix)
① 2 × 2 행렬의 헤세 행렬
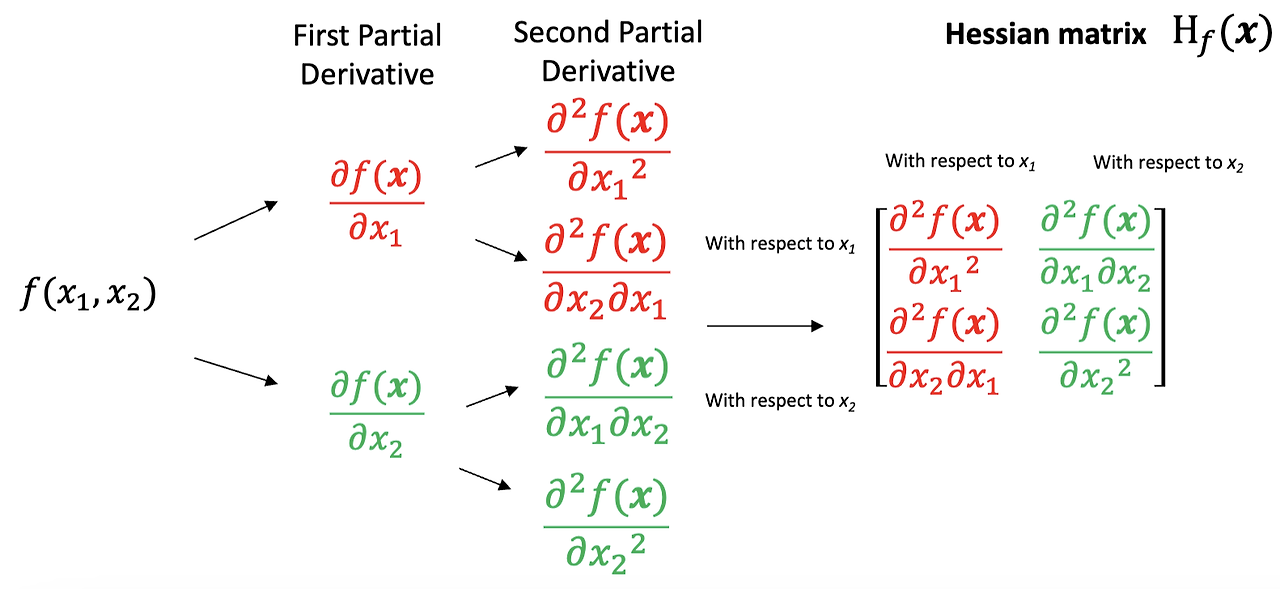
② 3 × 3 행렬의 헤세 행렬
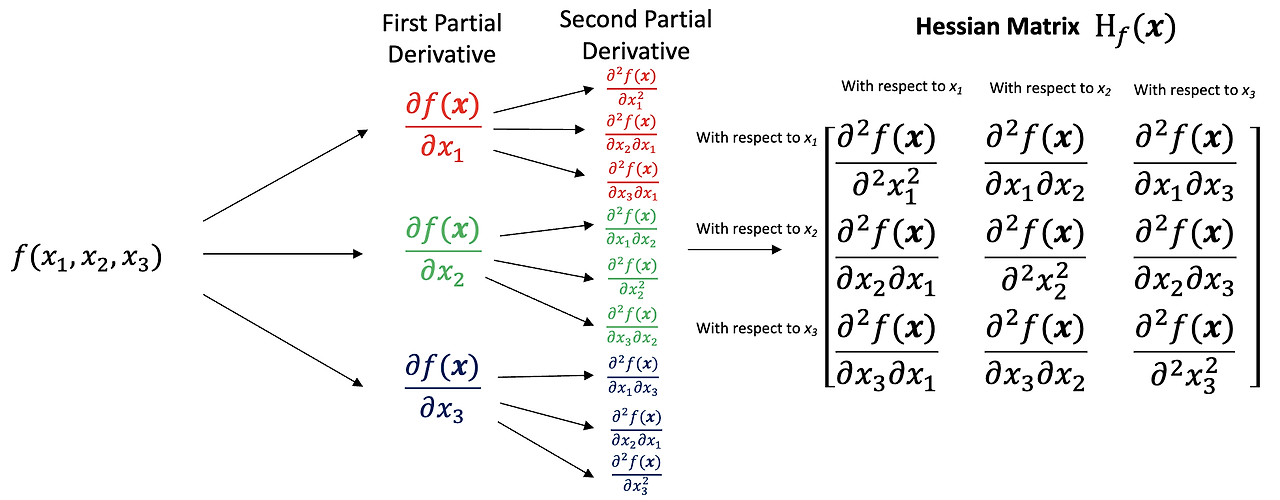
③ n × n 행렬의 헤세 행렬
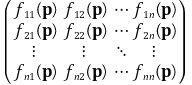
2. 미분방정식과 고유치 [목차]
⑴ 연립 선형 상미분방정식 : 2 × 2 행렬 A로 표현되는 연립 선형 상미분방정식에 대하여,
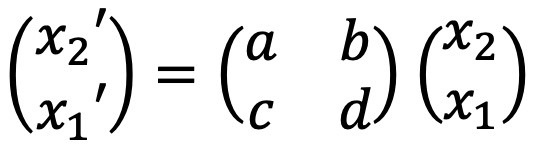
① 경우 1. A가 고유치 λ1, λ2를 갖고 대각화가 가능한 경우 : λ1, λ2와 각각 대응되는 고유벡터 v1, v2에 대해, 해는 다음과 같이 표현됨
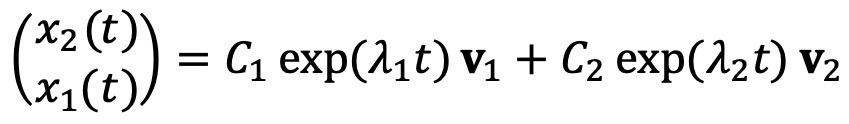
② 경우 2. A가 복소수 고유치 p ± qi를 갖는 경우 : 해는 다음과 같이 표현됨
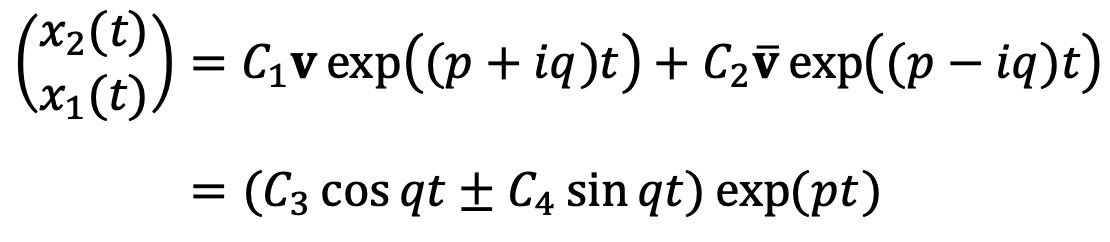
③ 경우 3. A가 다중도가 2인 고유치 λ 1개를 갖고 있고, 대각화가 안 된다면 일반해 x는 일반화된 고유벡터와 함께 다음과 같음
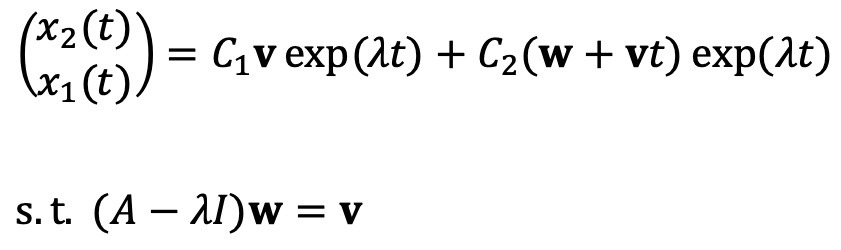
⑵ 선형 근사(linearization)
① 예제 : x' = x3 - y, y' = x인 경우 평형점(equilibrium point) (0, 0)의 분류
② 단계 1. 다음 근사식을 찾을 수 있음
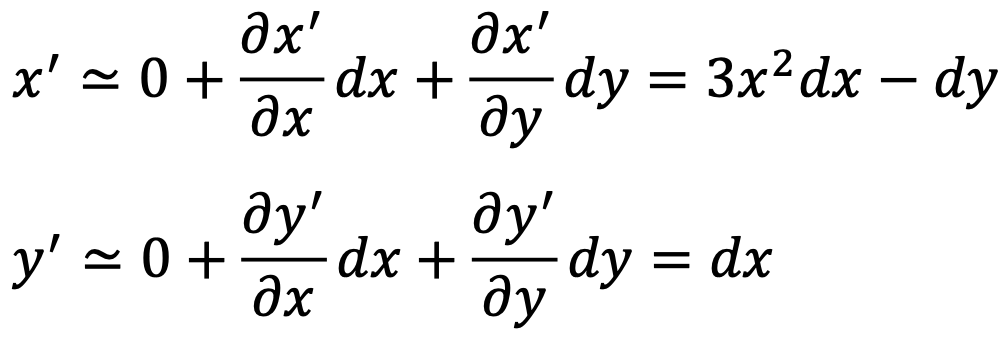
③ 단계 2. Jacobian 행렬 구성
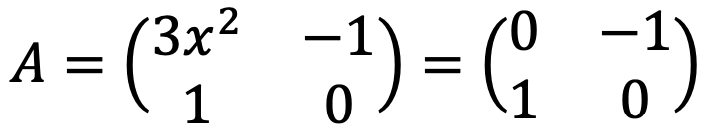
④ 단계 3. 고유치 계산
○ 고유치가 모두 음수인 실수인 경우 : 해당 평형점은 안정(stable)
○ 고유치가 하나는 양수이고 다른 하나는 음수인 경우 : 해당 평형점은 안장점(saddle)
○ 고유치가 모두 양수인 실수인 경우 : 해당 평형점은 불안정(unstable)
○ 고유치가 모두 복소수인 경우 : 해당 평형점은 spiral
○ A의 고유치는 ± i이므로 (0, 0) 주변에 spiral 패턴이 나타남
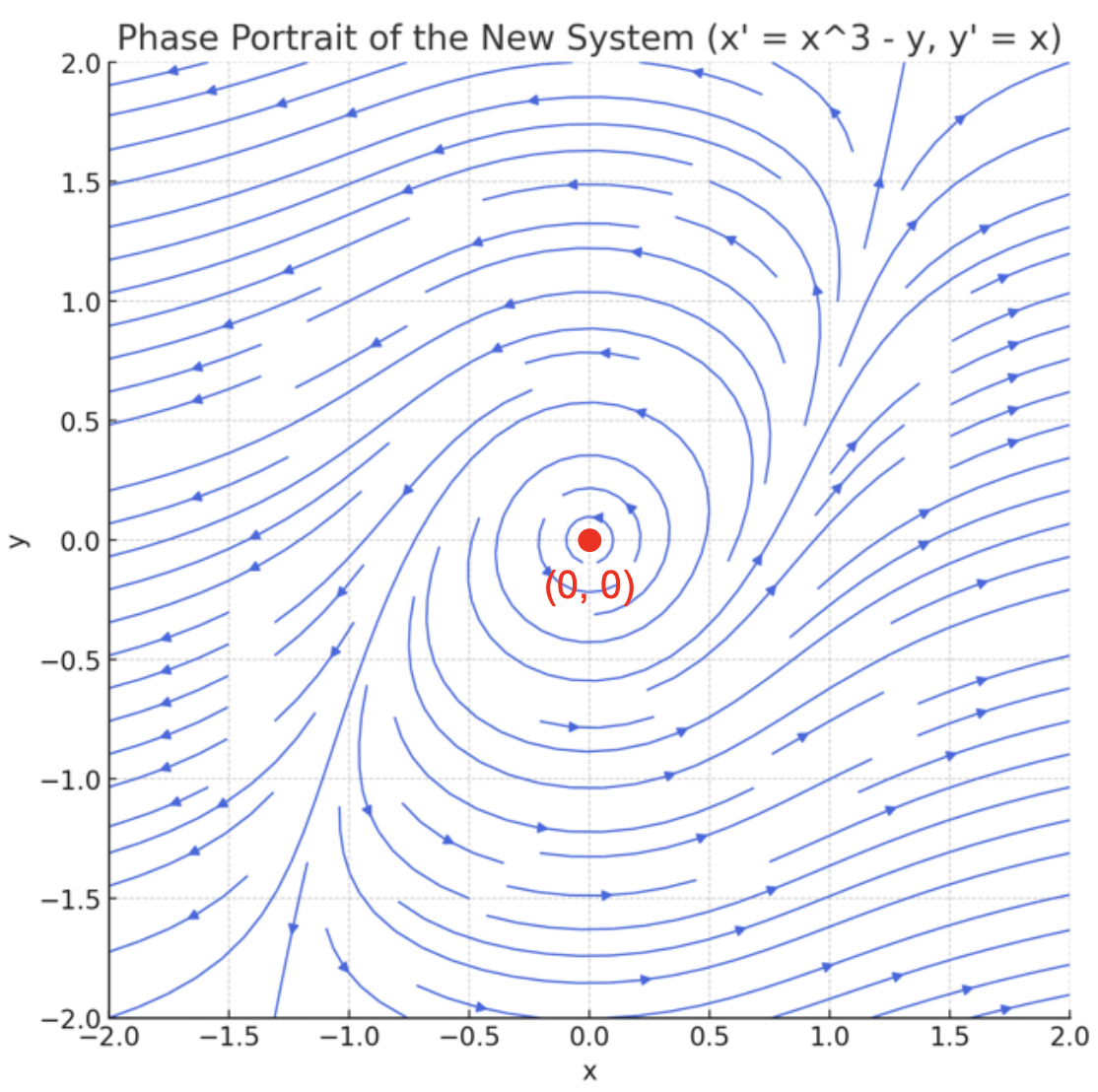
Figure. 1. 주어진 시스템의 유선도
입력: 2024.11.24 13:29
'▶ 자연과학 > ▷ 대수학' 카테고리의 다른 글
| 【선형대수학】 선형대수학 문제 [01-20] (0) | 2024.12.29 |
|---|---|
| 【선형대수학】 선형대수학 문제 [21-40] (0) | 2024.12.26 |
| 【수능】 2024년도 수능 수학 22번 풀이 (1) | 2023.11.21 |
| 【대수학】 대수학 기초 문제 [21~40] (0) | 2023.08.26 |
| 【대수학】 대수학 기초 문제 [01~20] (2) | 2023.08.22 |



최근댓글