선형대수학 문제 [21-40]
추천글 : 【선형대수학】 선형대수학 목차
문제 21. 다음과 같은 행렬 A에 대해, A2022 = kA + ℓI, (k, ℓ은 실수)를 만족할 때, k + ℓ을 구하시오. 단, I는 2차 항등행렬(identity matrix)이다.

다음과 같은 점화식을 찾을 수 있다.
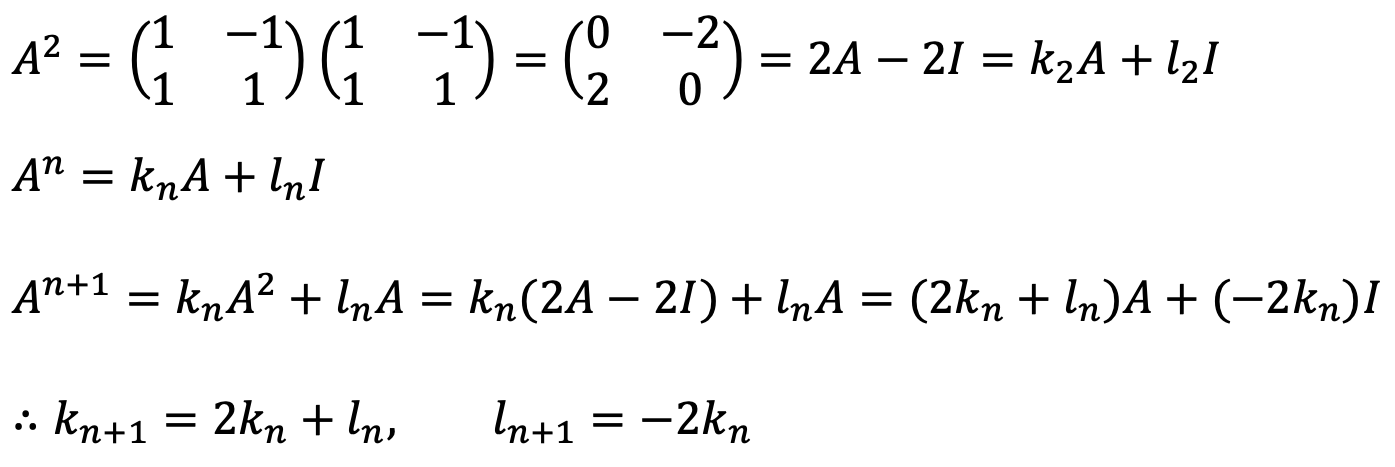
이제 일반항의 패턴을 알기 위해 다음과 같이 표를 구성하자.
| n | kn | ℓn | kn + ℓn |
| 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 2 | 2 | -2 | 0 |
| 3 | 2 | -4 | -2 |
| 4 | 0 | -4 | -4 |
| 5 | -4 | 0 | -4 |
| 6 | -8 | 8 | 0 |
| 7 | -8 | 16 | 8 |
| 8 | 0 | 16 | 16 |
| 9 | 16 | 0 | 16 |
| 10 | 32 | -32 | 0 |
| 11 | 32 | -64 | -32 |
| 12 | 0 | -64 | -64 |
| 13 | -64 | 0 | -64 |
| 14 | -128 | 128 | 0 |
그러므로 k2022 + ℓ2022 = 0이다.
문제 22. 다음을 풀어라.
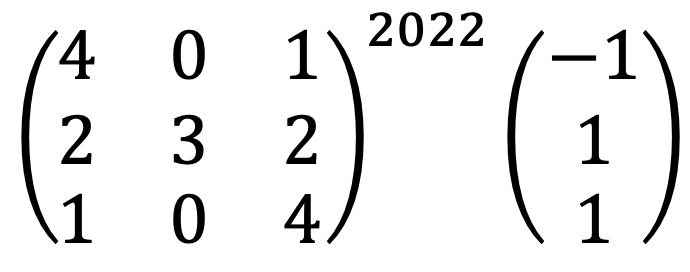
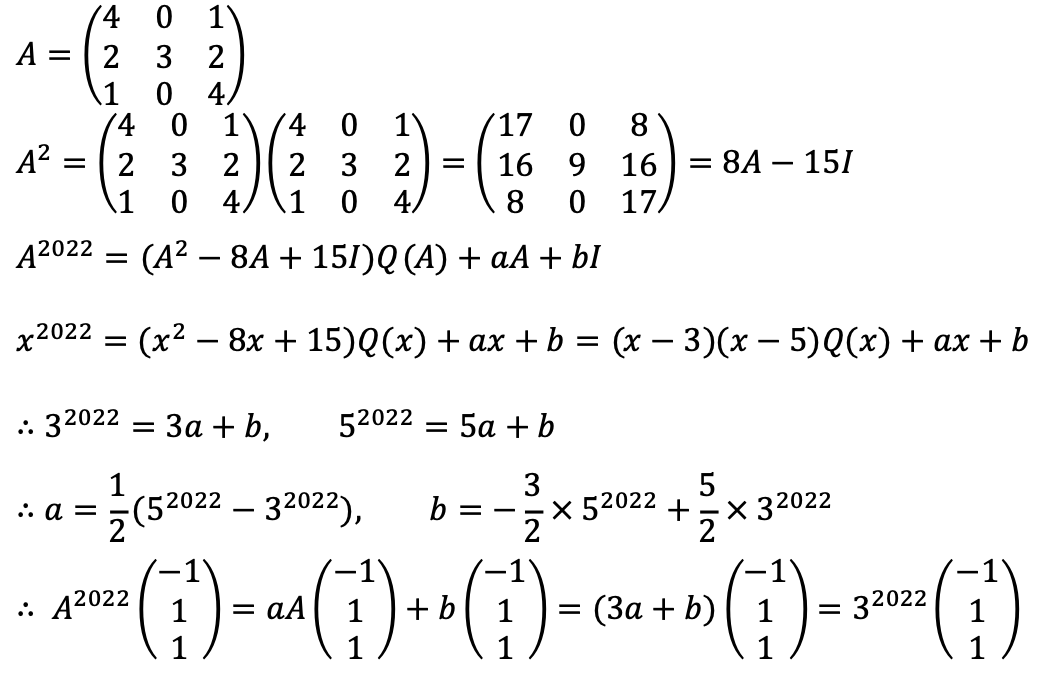
입력: 2024.12.25 13:48
'▶ 자연과학 > ▷ 대수학' 카테고리의 다른 글
| 【선형대수학】 선형대수학 문제 [01-20] (0) | 2024.12.29 |
|---|---|
| 【선형대수학】 5강. 선형대수학과 미적분 (0) | 2024.12.05 |
| 【수능】 2024년도 수능 수학 22번 풀이 (1) | 2023.11.21 |
| 【대수학】 대수학 기초 문제 [21~40] (0) | 2023.08.26 |
| 【대수학】 대수학 기초 문제 [01~20] (2) | 2023.08.22 |



최근댓글