4강. 고유치와 고유형식
추천글 : 【선형대수학】 선형대수학 목차
1. 고유치와 고유벡터 [본문]
2. 행렬의 대각화 [본문]
3. 이차형식 [본문]
1. 고유치와 고유벡터 [목차]
⑴ 고유치(고유값, eigenvalue)와 고유벡터(eigenvector)

① 대각화 가능성, spectral clustering 등에서 사용
② 정리 1. (A - λI)x = 0에서 A - λI가 non-zero kernel을 가질 필요충분조건은 det(A - λI) = 0
○ 증명 : rank-nullity theorem
③ 정리 2. A ∈ ℝ2×2의 고유치가 λ1, λ2일 때 A2 - (λ1 + λ2)A + λ1λ2I = O가 성립
○ 증명
고유치의 정의로부터 다음이 성립

이로부터 쉽게 λ1 + λ2 = a + d, λ1λ2 = ad - bc가 성립함을 앎
그러므로 케일리-헤밀턴 정리에 의해 준 명제가 성립함
이를 응용하여 An = (A - λ1I)(A - λ2I) Q(A) + kA + sE와 같이 An (단, n ≥ 2)을 계산할 수 있음
④ 정리 3. 크기가 n × n 행렬인 실행렬 A의 행렬식 det(A)는 고유치의 곱과 같음
○ 예를 들어, 3 × 3 행렬에 대해 보면 다음과 같음
○ A가 3개의 일차독립인 고유벡터를 가진다면, det(A)를 다음과 같이 보일 수 있음

○ 고유치가 λ1, λ2이고 각각 다중도(multiplicity)가 1, 2이라면, det(A)를 다음과 같이 보일 수 있음
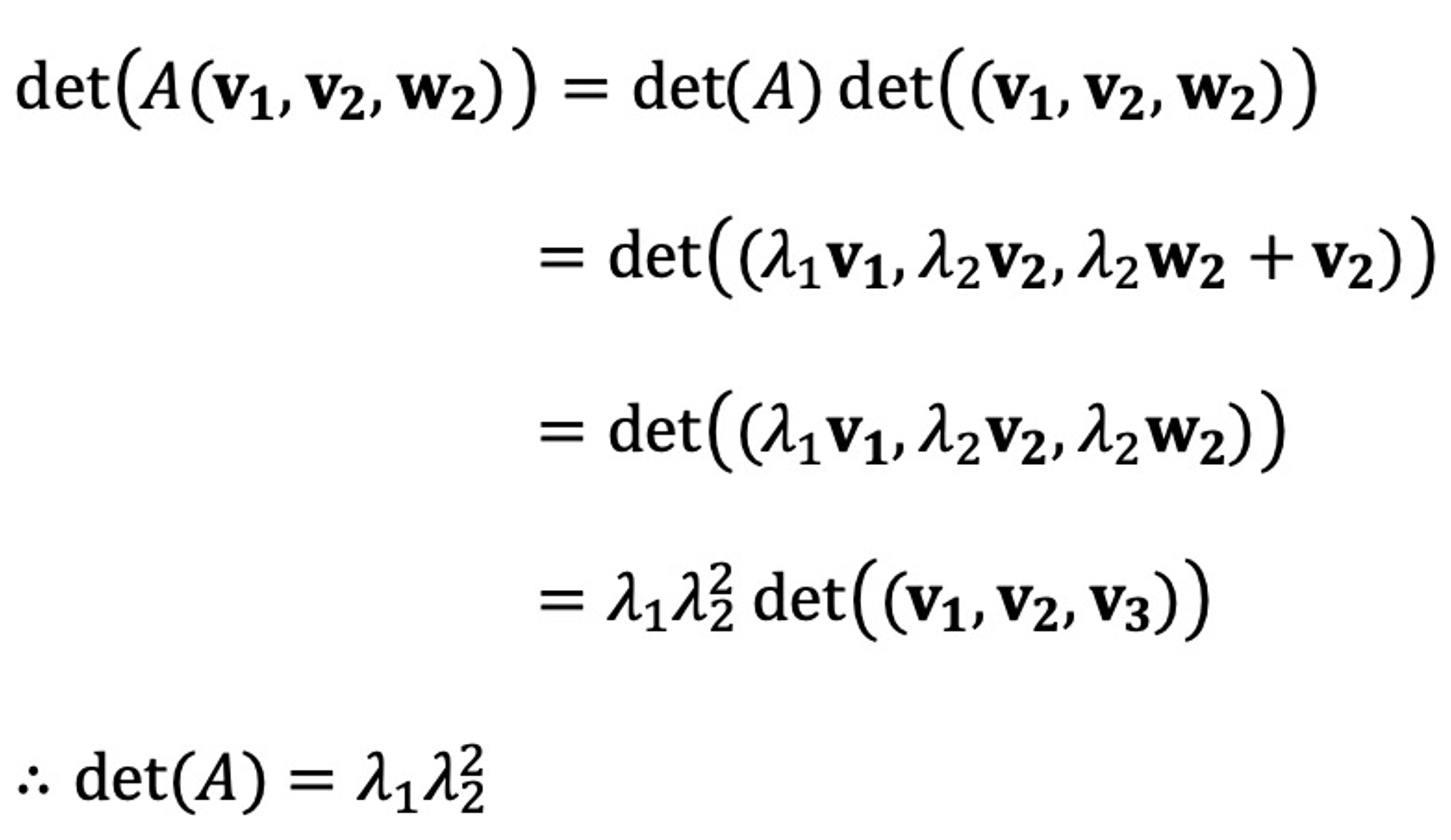
○ 단, w2는 λ2 및 v2에 대응되는 일반화된 고유벡터
○ 이런 식으로 각 경우에 대하여 따지면 고유치의 곱이 det(A)과 같음을 쉽게 보일 수 있음
⑤ 정리 4. 행렬의 대각화를 응용하면, A = PDP-1로부터 An = PDnP-1을 구할 수 있음
⑥ 정리 5. 크기가 n × n인 실행렬 A와 B에 대하여, 행렬 AB의 고윳값은 행렬 BA의 고유값이 됨 (ref)
○ 증명 : λ는 AB의 고유값이라고 가정
⇔ ABv = λv, v ≠ 0
⇔ BABv = BA (Bv) = B · λv = λ (Bv)
⇔ 다음과 같이 가능한 모든 경우를 고려해 보았을 때, BA의 고유값은 AB의 고유값과 동일함
○ Bv ≠ O인 경우 : λ는 BA의 고유값
○ Bv = O인 경우
⇔ ABv = AO = O = λv
⇔ λ = 0은 AB의 고유값
⇔ 0 = det(AB) = det(A) × det(B) = det(BA)
⇔ 따라서 BAv' = O인 v' ≠ 0이 존재함
⇔ λ = 0도 BA의 고유값
⑦ 정리 6. 크기가 m × n인 실행렬 A에 대하여, 행렬 AAT와 ATA의 0이 아닌 고윳값은 동일함 (ref)
○ 정리 5와 관련
⑧ 응용 1. 휘켈 근사와 해밀토니안
⑨ 파이썬 코드 (cf. WolframAlpha)
○ numpy 이용
import numpy as np
matrix = np.array([
[4.56, 10.2, 7.68, 13.68],
[10.2, 33.2, 20.2, 24.8],
[7.68, 20.2, 17.84, 23.44],
[13.68, 24.8, 23.44, 45.55]
])
eigenvalues, eigenvectors = np.linalg.eigh(matrix)
sorted_indices = np.argsort(eigenvalues)[::-1]
sorted_eigenvalues = eigenvalues[sorted_indices]
sorted_eigenvectors = eigenvectors[:, sorted_indices]
print("Eigenvalues:\n", sorted_eigenvalues)
print("\nEigenvectors:\n", sorted_eigenvectors)
○ sympy 이용
from sympy import Matrix
# SymPy 행렬 생성
matrix = Matrix([
[4.56, 10.2, 7.68, 13.68],
[10.2, 33.2, 20.2, 24.8],
[7.68, 20.2, 17.84, 23.44],
[13.68, 24.8, 23.44, 45.55]
])
# 고유값과 고유벡터 계산
eigenvalues = matrix.eigenvals() # 고유값 계산
eigenvectors = matrix.eigenvects() # 고유벡터 계산
# 출력
print("Eigenvalues:")
for eigval, multiplicity in eigenvalues.items():
print(f"Value: {eigval}, Multiplicity: {multiplicity}")
print("\nEigenvectors:")
for eigval, eigen_mult, eigvecs in eigenvectors:
print(f"Eigenvalue: {eigval}")
for vec in eigvecs:
print(f"Eigenvector: {vec}")
⑵ 일반화된 고유벡터(generalized eigenvector)
① 개요
○ 정의 : 비대칭 행렬의 대수적 중복도보다 기하적 중복도가 작을 때, 모자라는 고유벡터들을 대신하는 벡터들
○ 행렬 A의 rank m의 일반화된 고유벡터는 다음과 같음
(A - λI)mxm = 0 & (A - λI)m-1xm ≠ 0
○ m = 1인 경우 고유벡터의 정의와 동일함
○ 조르단 표준형에서 사용됨
② 예시 1. 다음 행렬 A의 고유치는 1이고 그와 대응하는 고유벡터는 v1 = (1, 0)T
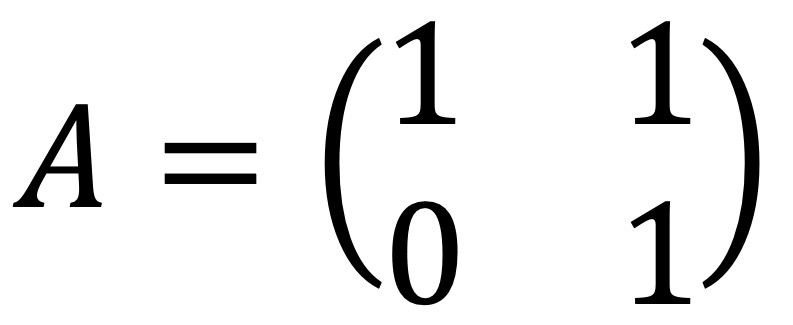
○ 고유치 1의 대수적 중복도는 2이고 기하학적 중복도는 1
○ (A - λI)2 v2 = (A - λI) {(A - λI) v2} = 0 ⇔ (A - λI) v2 = v1
○ (A - I)v2 = (1, 0)T를 만족하는 v2 = (*, 1)T (e.g., (0, 1)T)를 일반화된 고유벡터라고 함
③ 예시 2
⑶ 고유함수(eigenfunction)
① Sturm-Liouville의 정리 : 서로 다른 고유함수끼리는 직교함
2. 행렬의 대각화 [목차]
⑴ 대각행렬(diagonal matrix)
① 대각선 이외의 성분은 전부 0인 n × n 행렬
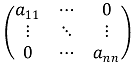
② 성질
○ 성질 1. 행렬식은 대각선 성분들의 곱
○ 성질 2. 역행렬은 주어진 대각행렬의 각 대각선 성분들이 역수인 행렬
⑵ 블록 대각행렬(block diagonal matrix)
① 정의 : Ai ∈ ℳni,ni (F)일 때 (단, i = 1, ···, k), n1 + ··· + nk = n일 때 다음과 같은 형태의 행렬 A를 지칭함
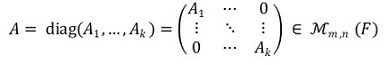
② 성질 : Ai, Bi ∈ ℳni,ni (F)일 때,
○ 성질 1. diag(A1, ···, Ak)·diag(B1, ···, Bk) = diag(A1B1, ···, AkBk)
○ 성질 2. Ai가 가역이면, (diag(A1, ···, Ak))-1 = diag(A1-1, ···, Ak-1)
⑶ 대각화 가능성
① 정의 : 다음을 만족하는 대각행렬 D, 정칙행렬 P가 있다면 A는 대각화가 가능(diagonalizable)하다고 함
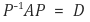
② 직교대각화(orthogonal diagonalization) : 정규직교기저로 구성된 행렬 P에 대해
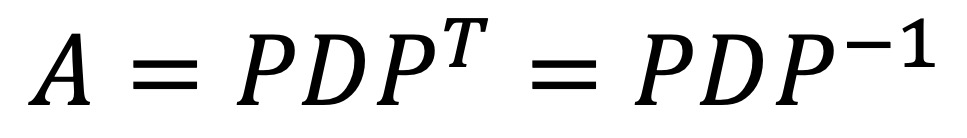
③ 정리 1. n × n 행렬 A가 대각화 가능하기 위한 필요충분조건은 A가 n개의 일차독립인 고유벡터를 가짐
④ 정리 2. n × n 행렬 A가 n개의 서로 다른 고유값 λ1, λ2, ···, λn을 가지면, A는 대각화가 가능함
○ P가 A의 선형독립인 고유벡터들을 열로 갖는 행렬이라 했을 때, 대각행렬 D는 다음과 같음
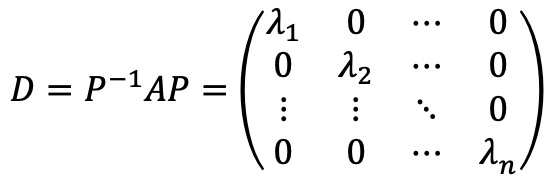
⑤ 정리 3. spectral theorem : n × n 행렬 A가 직교 대각화가 가능하기 위한 필요충분조건은 A가 대칭행렬(symmetric)인 것
⑥ 정리 4. n × n 행렬 A의 일반화된 고유벡터들은 항상 ℝn을 span하므로, 그러한 행렬 A는 대각화가 가능함
○ 예 : A2 = A인 n × n 행렬은 λ = 0, 1의 고유치를 가지며 대각화 가능함
⑦ 정리 5. 서로 다른 세 대각 원소를 가지는 대각행렬 D와 가환(commutant)하는 행렬도 대각행렬이 됨
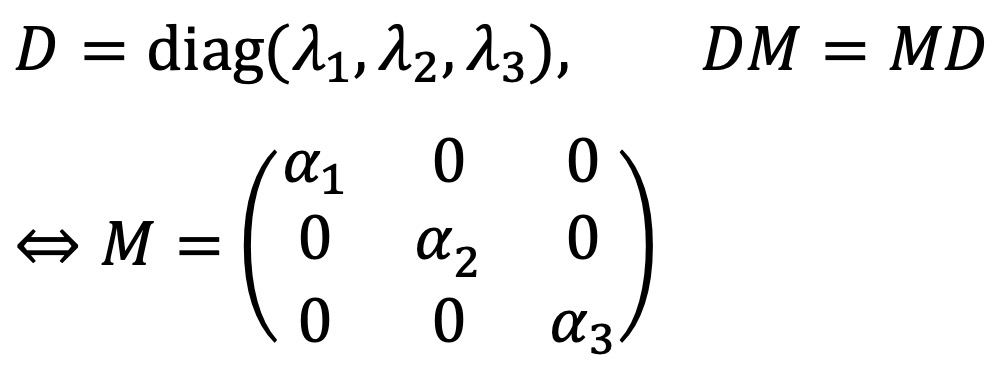
⑷ 조르단 표준형(Jordan canonical form)
① 행렬이 대각화 가능하지 않지만, 여전히 고유값에 대응하는 일반화된 고유벡터가 존재하는 경우에는 조르당 표준형으로 변환할 수 있음
② 조르당 표준형 : A = PJP-1 (단, J는 완전한 대각행렬은 아니고, 조르당 블록으로 이루어진 행렬)
③ 정리 1. Ak = O (nilpotent)는 행렬 A의 Jordan 형식을 생각하면, A는 적당한 Ak들로 이루어진 볼록대각행렬이 됨
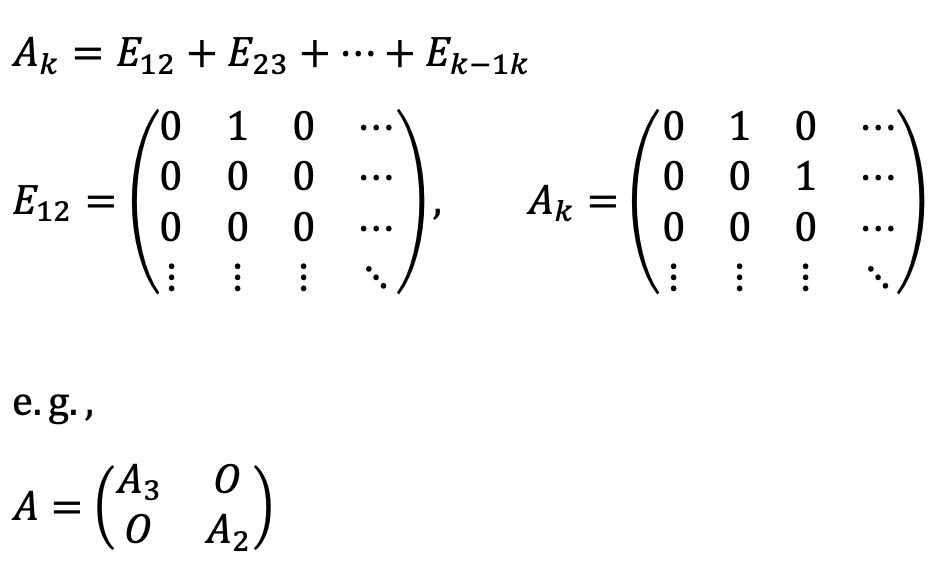
⑸ 예제
① 행렬 A가 주어져 있음
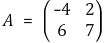
② 고유치와 고유벡터 계산
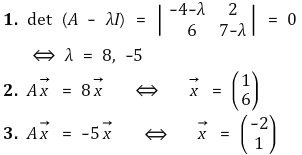
③ P와 D의 계산
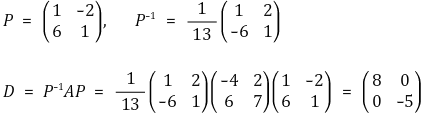
3. 이차형식(quadratic form) [목차]
⑴ 정의 : 4x12 + 2x1x2 + 3x22은 이차형식이지만, 4x12 + 2x1은 이차형식이 아님
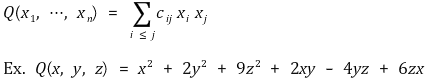
⑵ 대칭행렬을 이용한 표현
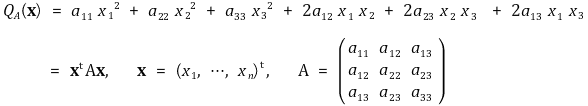
⑶ 이차형식의 부호 정의 : 대칭행렬 A ∈ ℳn와 ℝn상의 모든 벡터 x ≠ 0에 대하여
① 양정부호 행렬(positive definite matrix)
○ A의 모든 고유치가 0보다 큼 ⇔ Q(x) > 0 ∀x ≠ 0 ⇔ xtAx = xt(λx) = λ|x|2 > 0
② 양반정부호 행렬(positive semi-definite matrix)
○ A의 모든 고유치가 0보다 크거나 같음 ⇔ Q(x) ≥ 0 ∀x ≠ 0 ⇔ xtAx = xt(λx) = λ|x|2 ≥ 0
③ 음정부호 행렬(negative definite matrix)
○ A의 모든 고유치가 0보다 작음 ⇔ Q(x) < 0 ∀x ≠ 0 ⇔ xtAx = xt(λx) = λ|x|2 < 0
④ 음반정부호 행렬(negative semi-definite matrix)
○ A의 모든 고유치가 0보다 작거나 같음 ⇔ Q(x) ≤ 0 ∀x ≠ 0 ⇔ xtAx = xt(λx) = λ|x|2 ≤ 0
⑤ 부정부호 행렬(indefinite matrix)
○ ① ~ ④와 달리 부호가 일정하지 않은 경우. A의 고유치 중 부호가 다른 게 존재
⑥ 정리 1.

○ 증명 : 대칭행렬인 A는 직교대각화를 할 수 있으므로 (∵ spectral theorem)
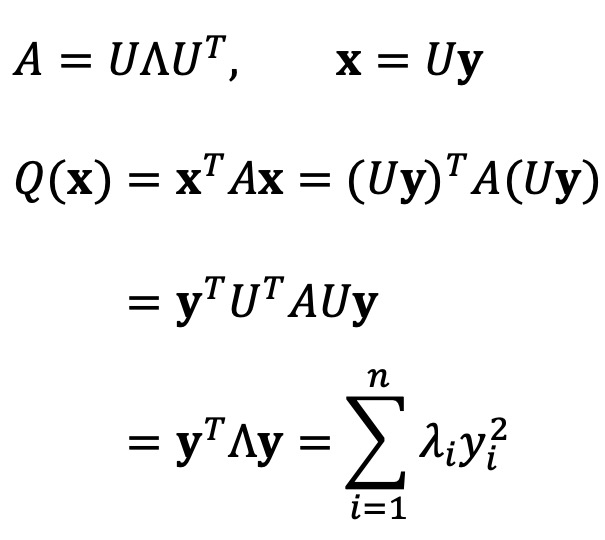
⑷ 이차형식의 부호 판정 : 대칭행렬 A ∈ ℳn과 {1, 2, ···, n}의 부분집합 S ={i1, i2, ···, ik}에 대하여
① 주소행렬(principal submatrix) : A에서 S에 해당하는 순서의 행과 열을 선택한 k × k 행렬
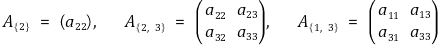
② 선도주소행렬(leading principal submatrix) : A의 마지막 n-k개의 행벡터와 열벡터를 생략하고 남은 k × k 행렬
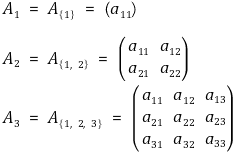
③ 정리 1. 대칭행렬 A ∈ ℳn가 양정부호인 것과 sgn(det(Ak)) = 1, k = 1, 2, ···, n인 것은 필요충분조건
④ 정리 2. 대칭행렬 A ∈ ℳn가 음정부호인 것과 sgn(det(Ak)) = (-1)k, k = 1, 2, ···, n인 것은 필요충분조건
⑤ 정리 3. 대칭행렬 A ∈ ℳn가 양반정부호인 것과 A의 모든 주소행렬식이 0 이상인 것은 필요충분조건
○ (주석) 정리 1 또는 2를 시도할 때 어느 선도주소행렬식이 0인 경우 정리 3을 시도함
○ 명백히 선도주소행렬식의 부호가 바뀌는 경우 부정부호행렬로서 정리 3 또는 4를 시도하지 않아도 됨
⑥ 정리 4. 대칭행렬 A ∈ ℳn가 음반정부호인 것과 -A의 모든 주소행렬식이 0 이상인 것은 필요충분조건
○ (주석) 정리 3을 시도하다가 주소행렬식의 부호가 일정하지 않으면 정리 4를 시도함
⑦ (참고) sgn은 판별식을 직접 계산하여 부호를 확인했을 때 양의 값이면 1, 음의 값이면 -1을 나타냄
⑸ 영역 Ω ⊂ ℝn에서 정의된 C2 함수 f : Ω → ℝ이 점 p ∈ Ω에서 ∇f(p) = 0라 하면 다음이 성립
① Hf(p)가 양정부호행렬이면 f는 점 x = p에서 극소값을 가짐
② Hf(p)가 음정부호행렬이면 f는 점 x = p에서 극대값을 가짐
③ Hf(p)가 부정부호행렬이면 점 x = p는 f의 안장점
④ Hf(p)가 양반정부호행렬이면 f는 점 x = p에서 상대적 극소
⑤ Hf(p)가 음반정부호행렬이면 f는 점 x = p에서 상대적 극대
⑹ 제약이 부여된 이차형식의 부호 판별 : 대칭행렬 A ∈ ℳn와 B ∈ ℳm, n (n > m) (즉, m행 n열) 에 대하여 n차원 이차형식 QA(x) = xtAx에 선형제약{x ∈ ℝn | Bx = 0}가 부여되어 있다. 새로운 (m+n) × (m+n) 행렬 H를 다음과 같이 정의했을 때 다음 명제가 성립한다.
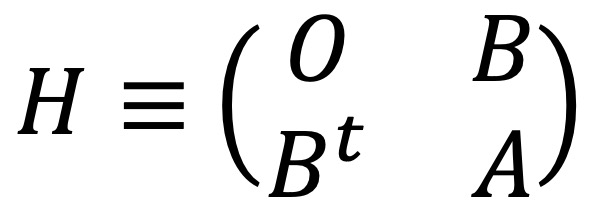
① 정리 1. sgn(|Hm+i|) = (-1)m, i = m+1, m+2, ···, n이면 QA(x) > 0이 성립
○ (주석) 필요충분조건이 아님을 유의
② 정리 2. sgn(|Hm+i|) = (-1)i, i = m+1, m+2, ···, n이면 QA(x) < 0이 성립
○ (주석) 필요충분조건이 아님을 유의
③ 예제 : 다음 예제는 음정부호인 대칭행렬 A를 보고 있음
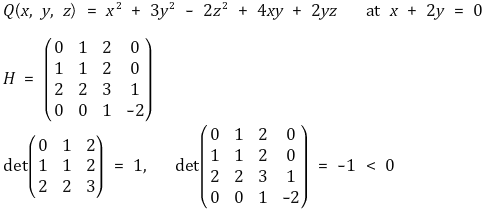
④ (참고) 부호가 없는 이차형식이라도 일정한 제약 하에서 부호를 가질 수 있음
입력: 2020.05.19 23:48
수정: 2024.11.12 09:45
'▶ 자연과학 > ▷ 대수학' 카테고리의 다른 글
| 【대수학】 대수학 기초 문제 [21~40] (0) | 2023.08.26 |
|---|---|
| 【대수학】 대수학 기초 문제 [01~20] (2) | 2023.08.22 |
| 【선형대수학】 3강. 행렬식과 역행렬 (0) | 2020.04.07 |
| 【선형대수학】 2강. 행렬의 계수 (0) | 2020.04.07 |
| 【선형대수학】 1강. 벡터공간 (0) | 2020.04.06 |




최근댓글