【ASA】 미국 보험계리사 P Exam 공식 암기 리스트

미국 보험계리사 P Exam 공식 암기 리스트 

 

추천글 : 【ASA】 ASA 시험 목차 

---

1. 확률공간 [본문]

2. 단변량 통계 분포 [본문]

3. 다변량 통계 분포 [본문]

4. 보험과 위험 관리 [본문]

5. 지참할 수 있는 계산기 종류 [본문]

---

계산기를 지참할 수 있고 종이와 펜이 주어짐

---

 

1. 확률공간 [목차]

⑴ 기초 확률 관계식 

① 포함·배제의 원리 : Pr(A ∪ B) = Pr(A) + Pr(B) - Pr(A ∩ B)

② Pr(A ∪ B ∪ C) = Pr(A) + Pr(B) + Pr(C) - Pr(A ∩ B) - Pr(B ∩ C) - Pr(A ∩ C) + Pr(A ∩ B ∩ C)

③ Pr(A^c) = 1 - Pr(A)

⑵ 전확률의 법칙(law of total probability) 

① Pr(B) = ∑_i=1,...,n Pr(B ∩ A_i)

⑶ 드 모르간 법칙(De Morgan's law)

① Pr[(A ∪ B)^c] = Pr(A^c ∩ B^c)

② Pr[(A ∩ B)^c] = Pr(A^c ∪ B^c) 

⑷ 조건부 확률(conditional probability) 

① Pr(A | B) = Pr(A ∩ B) / Pr(B)

⑸ 사건의 독립(independence)

① Pr(A ∩ B) = Pr(A)·Pr(B) 

② Pr(A | B) = Pr(A)

⑹ 베이즈 정리(Bayes' theorem)

① Pr(A_k | B) = Pr(B | A_k)·Pr(A_k) / ( ∑_i=1,...,n Pr(B | A_i)·Pr(A_i) )

⑺ 조합론(combinatorics)

① n! = n·(n-1)·...·2·1

② _nP_k = n! / (n-k)!

③ _nC_k = n! / ( (n-k)!·k! )

④ 분할(partition) = n! / ( k₁!·k₂!·...·k_r! ) s.t. k₁ + k₂ + ... + k_r = n

 

 

2. 단변량 통계 분포 [목차]

⑴ 확률변수와 분포

① 확률질량함수(probability mass function, PMF)

○ ∑_{all x} p_X(x) = 1

○ Pr(X = a) = 0 (단, 연속확률분포에 한정)

② 누적분포함수(cumulative distribution function, CDF)

○ F_X(x) = Pr(X ≤ x) = ∑_i≤x p_X(i) 

○ Pr(a < X ≤ b) = F_X(b) - F_X(a) 

○ f_X(x) = d/dx F_X(x) (단, 연속확률분포에 한정)

○ S_X(x) = 1 - F_X(x) = Pr(X > x)

③ 기댓값(expected value) : 이때 대괄호 [ · ] 를 사용함

○ E[g(X)] = ∫_{-∞ to ∞} g(x)·f_X(x) dx

○ E[g(X)] = ∫_{-∞ to ∞} g'(x)·S_X(x) dx, if g(-∞) = 0 (∵ 부분분수법)

○ E[g(X) | j ≤ X ≤ k] = ∫_{j to k} g(x)·f_X(x) dx / Pr(j ≤ X ≤ k)

○ E[c] = c

○ E[c·g(X)] = c·E[g(X)]

○ E[g₁(X) + ··· + g_k(X)] = E[g₁(X)] + ··· + E[g_k(X)] 

④ 분산(variance), 표준편차(standard deviation), 변동계수(coefficient of variation)

○ Var[X] = E[(X - μ)²] = E[X²] - (E[X])² 

○ Var[aX + b] = a²·Var[X]

○ Var[c] = 0

○ SD[X] = √Var[X]

○ CV[X] = SD[X] / E[X]

⑤ 퍼센타일(percentile), 분위수(quantile) : 분위수 값이 커질수록 낮은 값

⑥ 모드(mode) : 확률값이 최대인 지점 

⑵ 이산확률분포(discrete probability distribution)

 

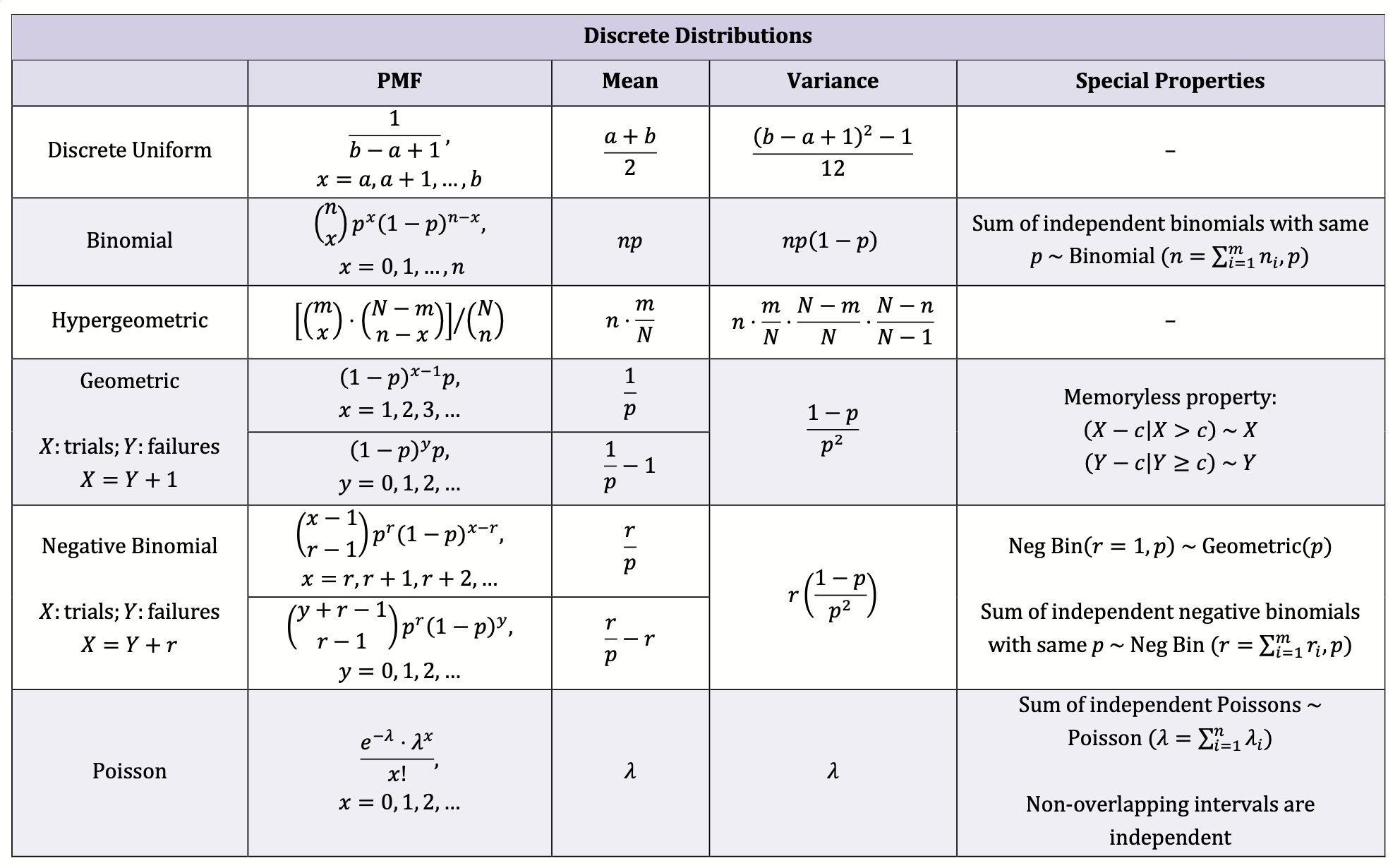
Table. 1. 이산확률분포

 

⑶ 연속확률분포(continuous probability distribution)

 

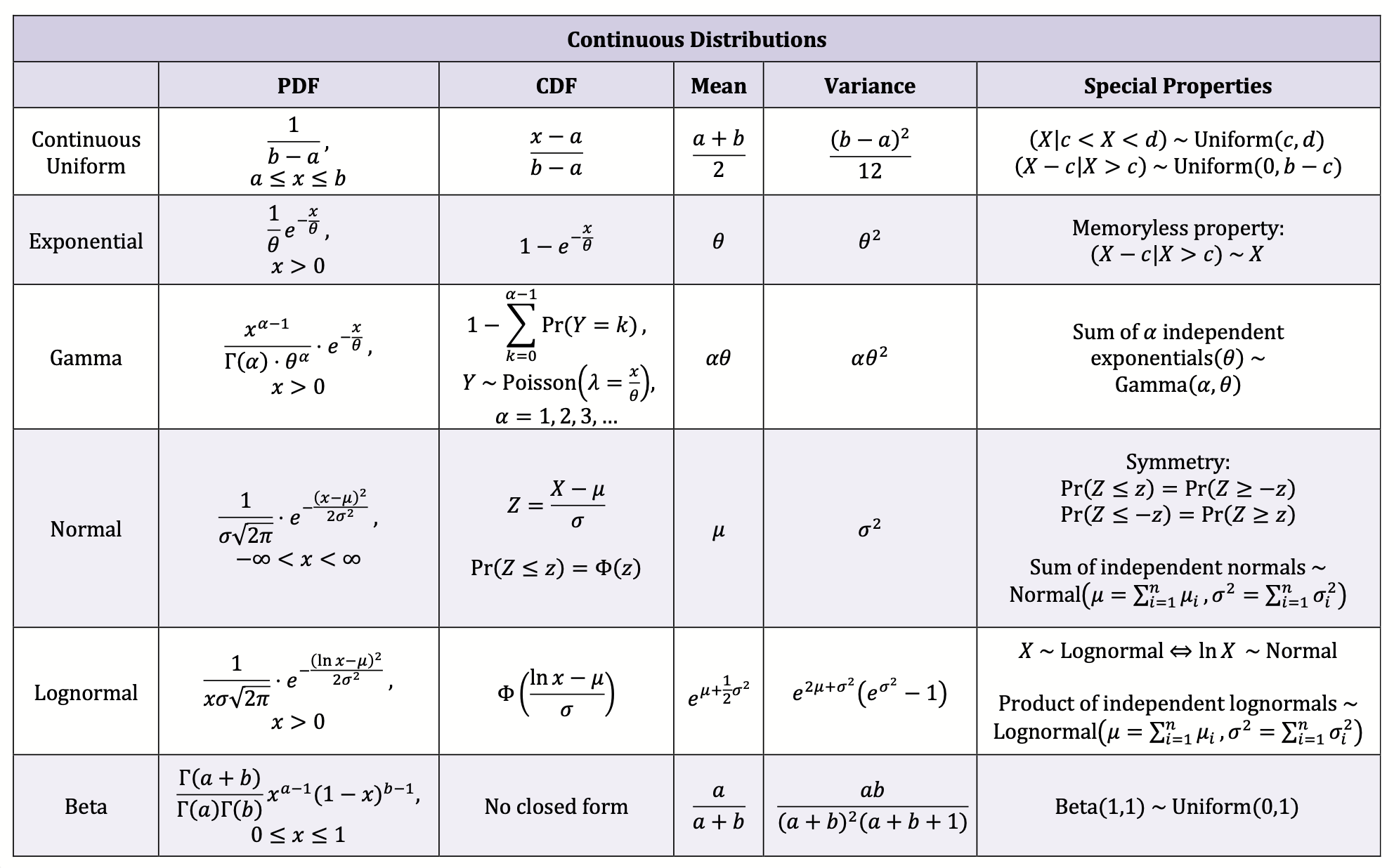
Table. 2. 연속확률분포

 

 

3. 다변량 통계 분포 [목차]

⑴ 결합 확률 분포의 PMF, CDF

① ∑_{all x} ∑_{all y} p_X,Y(x, y) = 1 

② F_X,Y(x, y) = ∑_s≤x ∑_t≤y p_X,Y(s, t)

③ F_X,Y(x, u_Y) = F_X(x)

④ F_X,Y(u_X, y) = F_Y(y)

⑤ S_X,Y(x, y) = Pr[(X > x) ∩ (Y > y)]

⑵ 주변부 확률 분포와 조건부 확률 분포

① p_X(x) = ∑_{all y} p_X,Y(x, y)

② p_Y(y) = ∑_{all x} p_X,Y(x, y)

③ p_X|Y(x | Y = y) = p_X,Y(x, y) / p_Y(y) 

⑶ 결합 확률 분포와 조건부 확률분포의 기댓값

① E[g(X, Y)] = ∑_{all x} ∑_{all y} g(x, y)·p_X,Y(x, y)

② E[X | Y = y] = ∑_{all x} x·p_X|Y(x | Y = y)

⑷ 가중 기댓값(weighted average)

① f_Y(y) = a₁f_C1(y) + a₂f_C2(y) s.t. Y = C₁ ∪ C₂, a₁ + a₂ = 1

② F_Y(y) = a₁F_C1(y) + a₂F_C2(y) s.t. Y = C₁ ∪ C₂, a₁ + a₂ = 1

③ S_Y(y) = a₁S_C1(y) + a₂S_C2(y) s.t. Y = C₁ ∪ C₂, a₁ + a₂ = 1

④ E[Y^k] = a₁E[C₁^k] + a₂E[C₂^k] 

⑸ 전분산의 법칙(law of total variance)

① E[X] = E[ E[X | Y] ]

② Var[X] = E[ Var[X | Y] ] + Var[ E[X | Y] ]

③ 예제

Let X have a binomial distribution with parameters 𝑛 and 𝑝, and let the conditional distribution of Y given X = x be Poisson with mean x. What is the variance of Y?

 

⑹ 공분산과 상관계수

① Cov[X, Y] = E[XY] - E[X]E[Y]

② Cov[aX, bY] = ab·Cov[X, Y]

③ Cov[X, X] = Var[X]

④ Var[aX + bY] = a²Var[X] + b²Var[Y] + 2ab·Cov[X, Y]

⑤ ρ_X,Y = Corr[X, Y] = Cov[X, Y] / √( Var[X]·Var[Y] )

⑺ 사건의 독립(independence) 

① F_X,Y(x, y) = F_X(x)·F_Y(y)

② f_X,Y(x, y) = f_X(x)·f_Y(y)

③ f_X|Y(x | y) = f_X(x)

④ f_Y|X(y | x) = f_Y(y)

⑤ E[h(X)·k(Y)] = E[h(X)]·E[k(Y)]

⑥ Cov[X, Y] = 0

⑦ ρ_X,Y = 0

⑻ 다항 분포(multinomial distribution)

① Pr(X₁ = x₁, ..., X_k = x_k) = n! / (x₁! · ... · x_k!) · p₁^x₁ · ... · p_k^x_k 

② E[X_i] = np_i

③ Var[X_i] = np_i(1 - p_i)

④ Cov[X_i, X_j] = -np_ip_j, i ≠ j

⑼ I.I.D 확률변수의 합과 평균

① S = X₁ + ... + X_n

② X̄ = [X₁ + ... + X_n] / n

③ E[S] = n·E[X_i]

④ E[X̄] = E[X_i]

⑤ Var[S] = n·Var[X_i]

⑥ Var[X̄] = (1/n)·Var[X_i] 

⑦ 중심극한정리(central limit theorem) : n이 충분히 크면 S와 X̄는 정규분포를 따름

⑽ 순서 통계량(order statistics)

① X_(k) = k-th order statistic

② X₍₁₎ = min(X₁, X₂, ..., X_n)

③ X_(n) = max(X₁, X₂, ..., X_n)

④ S_X(1)(x) = [S_X(x)]ⁿ s.t. i.i.d.

⑤ F_X(n)(x) = [F_X(x)]n s.t. i.i.d.

⑥ f_X(k)(x) = n · _n-1C_k-1 [F_X(x)]^k-1 · f_X(x) · [S_X(x)]^n-k = n! / ((k-1)! · (n-k)!) · [F_X(x)]^k-1 · f_X(x) · [S_X(x)]^n-k 

 

 

4. 보험과 위험 관리 [목차]

⑴ 보험과 위험 관리 : 부분적분법으로 E[Y]와 각 행의 두 번째 줄의 S_X(x)의 관계식을 증명할 수 있음

 

Table. 3. 보험과 위험 관리

 

⑵ X가 loss, Y가 payment (= reimbursed loss)라면, unreimbursed loss Z = X - Y → E[Z] = E[X] - E[Y]

 

 

5. 지참할 수 있는 계산기 종류 [목차]

⑴ Texas Instruments BA-35

⑵ Texas Instruments BA II Plus

⑶ Texas Instruments BA II Plus Professional

⑷ Texas Instruments TI-30X

⑸ Texas Instruments TI-30Xa

⑹ Texas Instruments TI-30X II (IIS solar or IIB battery)

⑺ Texas Instruments TI-30XB Multi View (battery)

⑻ Texas Instruments TI-30XS Multi View (solar)

 

입력: 2024.12.22 21:52