TransPhylo의 이해
추천글 : 【생물정보학】 생물정보학 분석 목차
1. 개요 [본문]
2. 역학 모델링 [본문]
3. 종결된 전염병 시나리오 [본문]
4. 진행중인 전염병 시나리오 [본문]
5. 최종 추론 [본문]
1. 개요 [목차]
⑴ 의의 : 부분적인 샘플링(partial sampling) 및 계속 진행중인 상태를 위한 역학 모델 (ref1, ref2)
⑵ 추론 전략 : 먼저 phylogenetic tree P를 계산하고, 그 뒤 T, θ, Neg를 추론하는 전략
① T : transmission tree
② θ : transmission tree와 샘플링 모델을 나타내는 파라미터 집합을 통틀어 이름
③ Neg : 숙주 내 병원체의 유전적 다양성. 감염 과정에서 이 다양성은 없어진다고 가정
⑶ Bayes' theorem

① 전염 트리 T가 이미 θ의 정보를 포함하기 때문에, P는 T를 통해 간접으로만 θ에 의존함
② 위 식에서 P(T | θ)를 구하는 것이 어려움
2. 역학 모델링 [목차]
⑴ α(k) : 자손이 k명일 확률. 음이항 분포로 정의됨

① k : 성공 횟수, 즉 감염된 개체가 전염을 성공한 횟수
② r : 실패 횟수, 즉 감염된 개체가 전염을 실패한 횟수. 고정된 값으로 감염된 개체가 전염을 전파할 수 있는 기본적인 강도를 의미함
③ p : 성공 확률, 즉 각 전염이 성공할 확률
3. 종결된 전염병 시나리오 [목차]
⑴ 샘플링에서 제외될 확률 : 재귀식으로 구성돼 있음
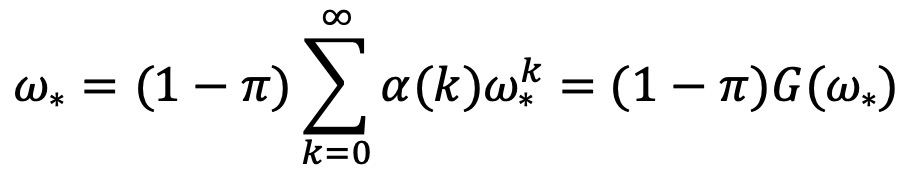
① ω* : 어떤 개체와 그 자손이 샘플링에서 제외될 확률. 위 식에 의해 바로 계산될 수 있는 값
② π : 샘플링 확률. 어떤 개체가 샘플링되지 않을 확률은 1 - π
③ G(z) : 음이항 분포의 확률 생성 함수. 참고로, 확률 생성 함수는 G(z) = 𝔼[zX] = M(ln z)으로 정의됨
④ 예 1. (1 - π) × α(0) : 0명의 자손을 남긴 개체가 전염 트리에 포함되지 않을 확률
⑤ 예 2. (1 - π) × α(1) × ω* : 1명의 자손을 남긴 개체가 전염 트리에 포함되지 않았고, 그 자손도 전염 트리에 포함되지 않을 확률
⑵ d명의 자손이 전염 트리에 포함될 확률
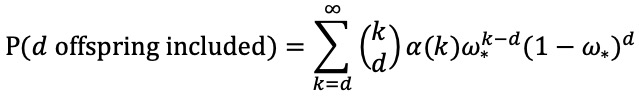
① d : 전염 트리에 포함된 자손의 수
② P(d offspring included) : d명의 자손이 전염 트리에 포함될 확률. k명의 총 자손 중 d명이 포함될 확률을 합산한 값
③ kCd·α(k) : 자손이 k명이고 k명의 총 자손 중 d명을 고르는 확률
④ ω*k-d(1 - ω*)d : 이미 정해진 d명은 샘플링이 됐고, 그렇지 않은 k - d명은 샘플링이 되지 않았을 확률
⑤ (1 - ω*)d가 고정항이기 때문에 계산의 단순화를 위해 해당 텀을 삭제함 : 최적화 알고리즘 결과에 전혀 영향을 안 줌
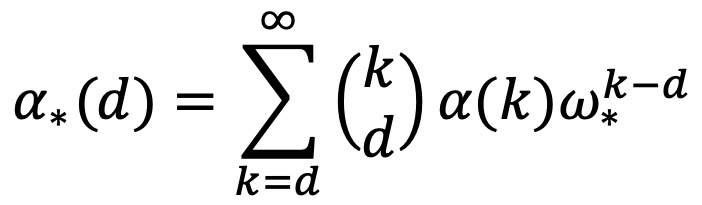
⑶ p*(T | θ)의 계산
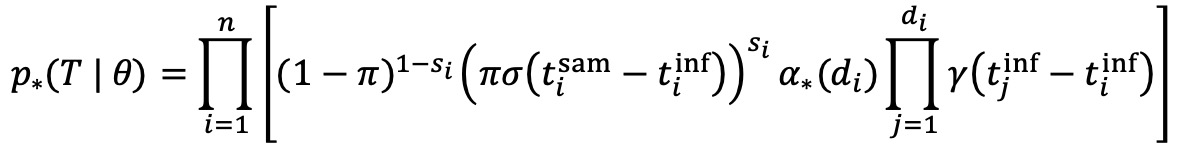
① n : 노드의 수. 감염된 개인의 수와 대응됨
② si : 그 개인이 샘플링되면 si = 1, 샘플링되지 않으면 si = 0
③ tisam : 그 i번째 개인이 샘플링된 시간
④ tiinf : 그 i번째 개인이 감염된 시간
⑤ σ : 샘플링 시간에 대한 확률밀도함수. si = 1일 때만 σ가 곱해지도록 (σ(tisam - tiinf))si를 고려하게 됨
⑥ α*(di) : i번째 개인이 감염시킨 di명의 개인이 전염 트리에 포함될 확률
⑦ γ : i번째 개인과 그 자가 감염시킨 다른 개인의 감염 시간 차이에 대한 확률밀도함수
4. 진행중인 전염병 시나리오 [목차]
⑴ 샘플링 확률 π 수정
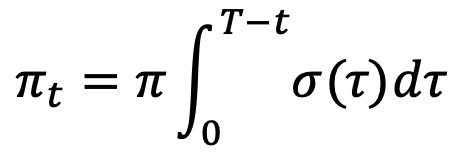
⑵ 샘플링에서 제외될 확률 ω 수정
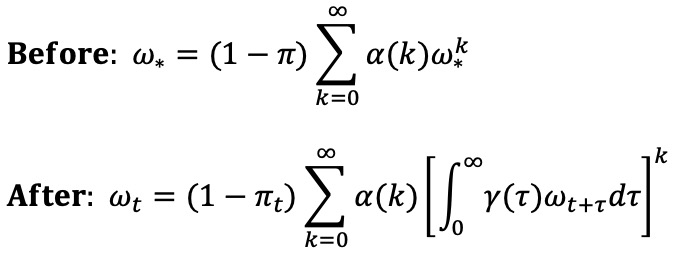
① γ(τ) : 감마함수
⑶ 자손함수 α 수정
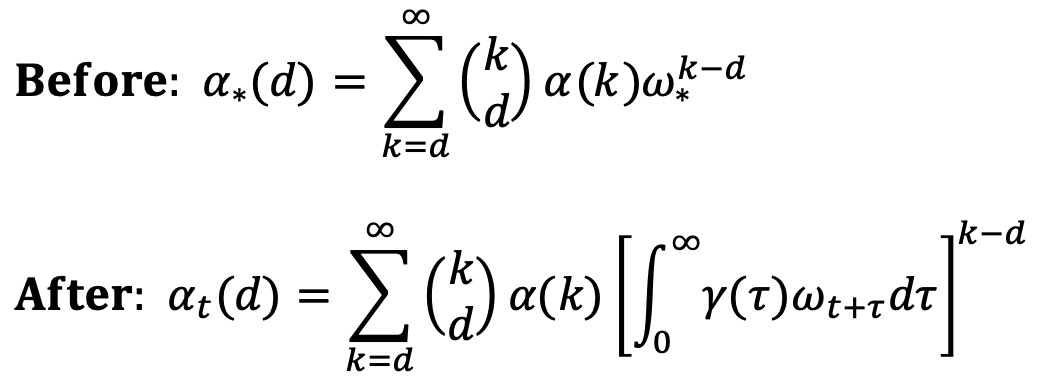
⑷ 전염트리 확률 P(T | θ) 수정
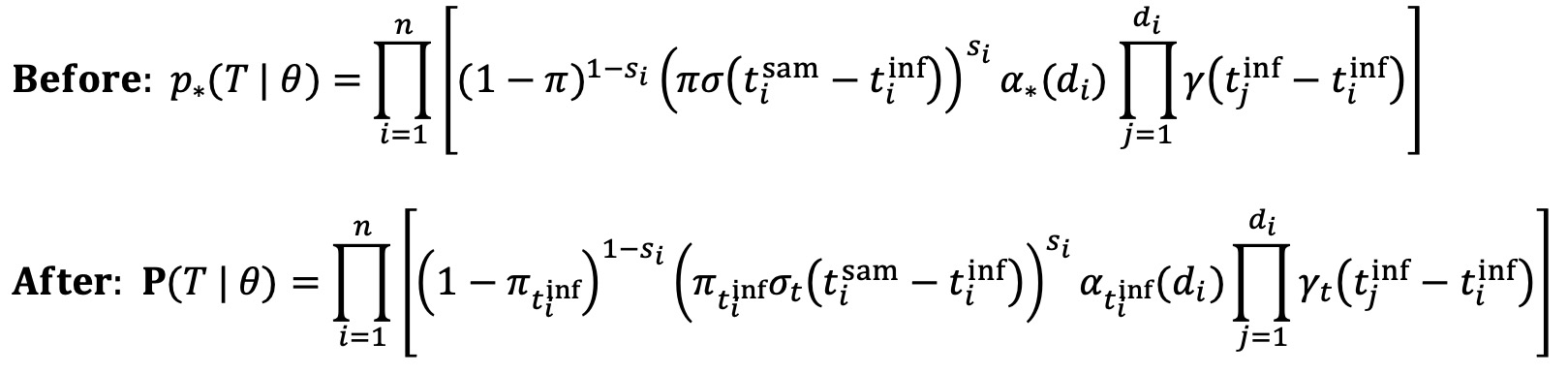
5. 최종 추론 [목차]
⑴ 전염 트리 모델의 정의
① 노드 : 각각의 노드는 감염된 개체를 나타냄
② 터미널 노드 : 샘플링된 감염 개체를 나타냄
③ 엣지 : 감염 간의 직접적인 전염 사건을 나타냄
④ 완전 전염 병목(bottleneck) : 전염 과정에서 단일 병원체 변이(single genomic variant)만이 전염되는 것으로 가정
⑵ 베이지안 추론을 통한 전염 트리 추정
① 두 확률 계산
○ P(T | θ) : 전염 트리의 사전 확률. 전염 모델 매개변수 θ에 의존
○ P(P | Neg, T) : 공통 계통 모델(coalescent model)을 사용하여 계산됨
② 계통수 색칠하기(coloring the phylogeny)
○ 각 숙주마다 고유의 색을 할당하여 계통수에서 전염 트리를 구성
○ 샘플링되지 않은 숙주가 있을 가능성을 고려하여, 색의 개수가 고정되지 않은 모델을 적용
③ MCMC를 통한 탐색
○ 전염 트리의 매개변수 공간을 MCMC를 사용하여 탐색
○ 트리에 새로운 전염 사건을 추가하거나 제거하는 reversible jump MCMC 방법을 사용함
⑶ MCMC 전환 확률
① MCMC 과정에서 새로운 전염 사건을 추가하거나 제거할 때의 전환 확률은 다음과 같이 정의됨
② 새로운 전염 사건 추가
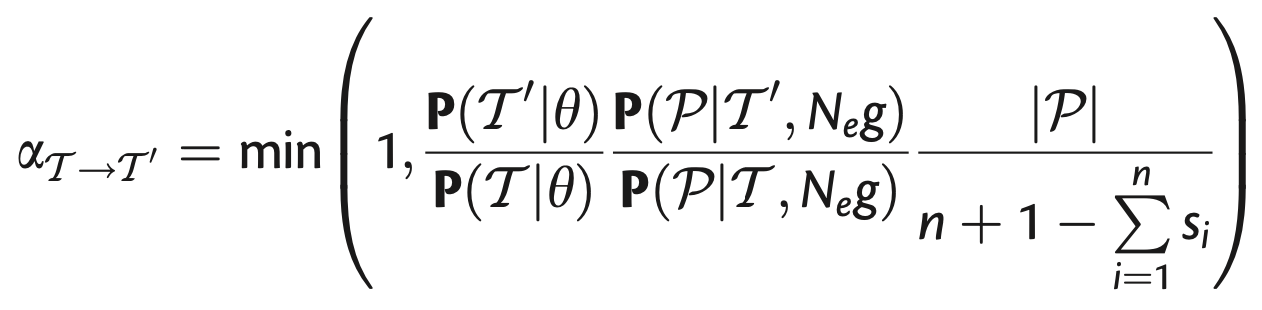
○ |P| : 계통수의 브랜치 길이의 합
○ n + 1 - ∑i=1 to n si : 새로 추가될 전염 사건의 가능한 위치 수
③ 전염 사건 제거
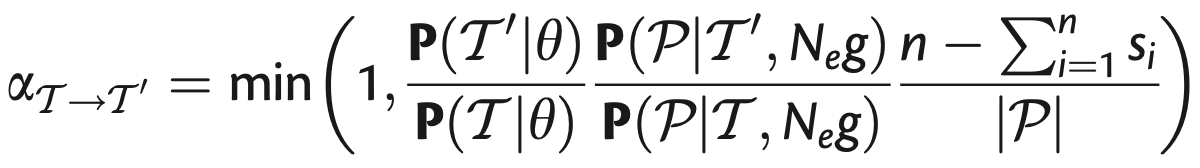
○ 제거할 수 있는 전염 사건의 개수와 계통수 길이의 비율로 가중치가 조정됨
⑷ 추론 과정의 추가 매개변수
① 음이항 분포의 첫 번째 매개변수 r : 사전분포로서 λ = 1인 지수분포를 사용
② 음이항 분포의 성공 확률 p : 사전분포로서 [0, 1] 구간의 균일분포를 사용
③ 샘플링 확률 π : 사전분포로서 [0, 1] 구간의 균일분포를 사용
④ 숙주 내 유효 집단 크기 Neg : 사전분포로서 λ = 1인 지수분포를 사용
입력: 2024.01.07 10:45
'▶ 자연과학 > ▷ 생물정보학' 카테고리의 다른 글
| 【생물정보학】 생물정보학 분석 목차 (5) | 2025.04.06 |
|---|---|
| 【생물정보학】 생물정보학 부록 (6) | 2025.02.20 |
| 【생물정보학】 리눅스 프로그래밍(bash programming) (0) | 2025.01.16 |
| 【생물정보학】 후성유전학 라이브러리 (4) | 2024.01.07 |
| 【생물정보학】 전사체 분석 파이프라인(Transcriptomics Pipeline) (23) | 2023.12.29 |


최근댓글