2강. 게임이론(game theory)
추천글 : 【미시경제학】 미시경제학 목차
1. 개요 [본문]
2. 동시게임 [본문]
3. 순차게임 [본문]
4. mixed strategy game [본문]
5. Bayesian game [본문]
6. 공약의 경제학 [본문]
1. 개요 [목차]
⑴ 플레이어(player) 또는 경기자 : 게임에 참가하는 경제적 주체. 기업, 소비자 등

⑵ 전략(strategy) : 각 플레이어들이 어떤 행동을 취할 것인가에 대한 계획

⑶ 페이오프(payoff) 또는 보수 : 각 플레이어들이 각자의 전략을 취함으로써 얻는 효용 또는 게임의 결과

① ui : i번째 플레이어의 효용, 즉 페이오프
② si : i번째 플레이어의 전략
③ s-i : 1, 2, ···, i-1, i+1, ···, n번째 플레이어의 전략
④ 일반적으로 표의 형태, 즉 보수행렬(payoff matrix)로 나타냄
⑷ 전략 프로파일(strategy profile) : 집합 (s1, ···, sn)을 지칭함
⑸ 게임(game) : 플레이어와 가능한 모든 전략과 페이오프들의 집합
⑹ 게임이론(game theory) : 전략 프로파일을 찾는 이론
⑺ BR(best response)
① 정의 : 한 플레이어에 대해 나머지 플레이어들의 전략을 고정했을 때 그 효용이 최대가 되도록 하는 전략
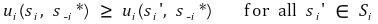
② 각 플레이어에게 효용이 동일한 전략이 여럿 있을 수 있어서 각 플레이어의 BR이 반드시 1개일 필요는 없음
⑻ 내쉬 균형(Nash equilibrium; NE)
① 정의 : 각 플레이어들의 전략이 모두 BR인 경우
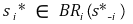
② 즉, 어느 플레이어도 자신의 선택을 바꾸지 않는 게 유리한 경우를 말함
③ (참고) 존 내쉬(John Nash) : 1994년 노벨경제학상 수상. 영화 뷰티풀 마인드의 주인공
⑼ 우월전략균형(dominant strategy equilibrium; DSE)
① 정의 : 모든 플레이어들이 dominant strategy를 취하는 경우
② 현실에서 흔하지 않다는 단점이 있음
③ 우월전략(dominant strategy) : 다른 플레이어들의 전략에 관계없이 그 플레이어의 효용이 최대가 되도록 하는 전략
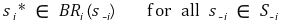
④ 정리 1. DSE ⊂ NE
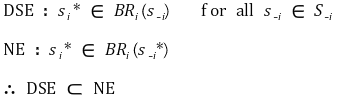
⑤ 정리 2. 우월전략균형이 존재하지 않아도 내쉬균형은 존재할 수 있음
○ 이유 : 내쉬균형을 위한 조건이 상대적으로 더 약하기 때문
2. 동시게임(simultaneous game) [목차]
⑴ 가정 : 협조가 불가능하고 게임이 단 한 번만 이루어짐
⑵ 표현 1. normal-form representation
① 예 1. match / mismatch game

Table. 1. match / mismatch game
○ 각 칸에 적힌 #, #에서 첫 번째 숫자는 1번째 플레이어의 효용, 두 번째 숫자는 2번째 플레이어의 효용을 의미
○ πi(si, s-i)는 i번째 플레이어가 si의 전략을, -i번째 플레이어가 s-i의 전략을 취했을 때 i번째 플레이어가 얻는 효용
○ 모든 BR을 확인하고 다음과 같이 표에 표시를 함

Table. 2. BR을 표시한 match / mismatch game
○ BR1(A ∈ S2) = B ∈ S1
○ BR1(B ∈ S2) = A ∈ S1
○ BR2(A ∈ S1) = A ∈ S2
○ BR2(B ∈ S1) = B ∈ S2
○ 각 칸에 적힌 #, #에서 모두 밑줄 쳐진 것은 없으므로 내쉬 균형은 없음
② 예 2. duopoly pricing game

Table. 3. duopoly pricing game
○ 각 칸에 적힌 #, #에서 첫 번째 숫자는 1번째 플레이어의 효용, 두 번째 숫자는 2번째 플레이어의 효용을 의미
○ πi(si, s-i)는 i번째 플레이어가 si의 전략을, -i번째 플레이어가 s-i의 전략을 취했을 때 i번째 플레이어가 얻는 효용
○ underlining method : 모든 BR을 확인하고 다음과 같이 표에 밑줄 표시를 함

Table. 4. BR을 표시한 duopoly pricing game
○ BR1(L ∈ S2) = L ∈ S1
○ BR1(H ∈ S2) = L ∈ S1
○ BR2(L ∈ S1) = L ∈ S2
○ BR2(H ∈ S1) = L ∈ S2
○ 내쉬 균형 : (s1, s2) = (L, L)
○ DSE : (s1, s2) = (L, L)
○ 1번째 플레이어의 dominant strategy는 L (∵ BR1(L ∈ S2) = L ∈ S1, BR1(H ∈ S2) = L ∈ S1)
○ 2번째 플레이어의 dominant strategy는 L (∵ BR2(L ∈ S1) = L ∈ S2, BR2(H ∈ S1) = L ∈ S2)
⑶ 표현 2. 게임나무 (extensive form) : 각 노드를 결정 노드(decision node)라고 함

Figure. 1. simultaneous game의 extensive form
duopoly game과 동일한 상황
3. 순차게임(sequential game) [목차]
⑴ 개요
① 특징 1. single-agent decision problem
○ 정의 : 한 플레이어가 다른 플레이어가 어떤 전략을 취하는지 전혀 무관하게 자신의 전략을 결정할 수 있는 경우
○ 일반적인 simultaneous game에서는 한 플레이어가 다른 플레이어의 전략에 영향을 받으므로 정의에 부합하지 않음
○ sequential game에서 주도권은 선 행위자에게 있으므로 single-agent decision problem에 해당함
○ (참고) simultaneous game도 sigle-agent decision problem일 수 있음 : 일방의 전략이 아무런 역할을 하지 않는 경우
② 특징 2. simultaneous game과 달리 action과 plan of actions의 개념이 구별됨
⑵ 예제
① sequential game의 normal-form representation : 비현실적인 내쉬 균형 해를 포함

Table. 5. sequential game의 normal-form representation
○ 상황 : Hardware 회사가 먼저 action을 취하고 Software 회사가 그 다음에 action을 취함
○ (HH, HS)의 의미 : Software 회사의 전략 중 하나로 Hardware 회사가 H이면 H를, S이면 H를 전략으로 하겠다는 의미
○ (S, (SH, SS))는 비현실적인 해 (∵ Hardware 회사는 당연히 H를 전략으로 취함)
② sequential game의 extensive form : 비현실적인 내쉬 균형 해를 포함하지 않음

Figure. 2. sequential game의 extensive form
③ (주석) simultaneous game과 달리 sequential game에서는 두 표현방법에 차이가 발생한다는 것도 중요한 특징
⑶ 적절한 서브게임(proper subgame)
① information set : 각 플레이어가 있을 수 있는 노드의 집합
○ Figure. 1.에서 Player 2의 information set은 한 개의 노드로 구성됨
○ Figure. 2.에서 Player 2의 information set은 두 개의 노드로 구성됨
② 적절한 서브게임 : extensive form으로 표현된 게임에서 singletone information set을 루트로 하는 트리
○ 즉, 하나의 게임 내에 있는 독립적인 게임을 지칭함
○ Figure. 2.은 총 세 개의 proper subgame이 존재함
③ 특징 1. 임의의 게임에 대해 전체 게임 그 자체로 하나의 서브게임이 됨
④ 특징 2. simultaneous game은 오직 한 개의 서브게임만 존재함
⑤ 특징 3. 그 루트에 해당하는 decision maker가 한 명이라는 점에서 single-agent decision problem의 특수한 예
⑷ SPE(subgame-perfect equilibrium)
① 정의 : 모든 proper subgame에 대해 내쉬 균형인 전략 프로파일(strategy profile)
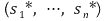
② (참고) 동시게임의 경우 내쉬균형 개념과 관련 있고, 순차게임의 경우 완전균형 개념과 관련 있음
③ 특징 1. SPE는 NE 중 하나가 돼야 함
④ 특징 2. NE라고 하여 반드시 SPE는 아닐 수 있음
○ 이유 : proper subgame에서는 비현실적인 내쉬 균형 해를 제거하므로
○ (주석) proper subgame은 extensive form을 통해 해를 찾는 방법으로 볼 수 있어 비현실적인 해를 포함하지 않음
⑸ forward induction : 위에서 아래로 SPE를 찾는 방법
① 1st. 모든 NE를 찾음
○ 위의 예제에서 (H, (HH, HS)), (H, (HH, SS)), (S, (SH, SS))를 찾을 수 있음
② 2nd. 모든 proper subgame에서 NE인지 아닌지를 확인함
○ (H, (HH, HS)) : Hardware 회사가 S를 취했을 때 나오는 서브게임에서 Software 회사는 H를 취하므로 부적절함
○ (H, (HH, SS)) : SPE가 맞음
○ (S, (SH, SS)) : Hardware 회사가 H를 취했을 때 나오는 서브게임에서 Software 회사는 S를 취하므로 부적절함
⑹ backward induction : 아래에 위로 SPE를 찾는 방법
① 1st. extensive form으로 표현된 sequential game에서 리프(leaf)부터 올라가 최초의 singleton information set을 찾음
② 2nd. 각 proper subgame에서 NE를 찾음
③ 3rd. 그 singleton information set에서 올라가 두 번째 singleton information set을 찾음
④ 4th. 각 proper subgame에서 NE를 찾은 뒤 적절하게 표시함
⑤ 5th. ③ ~ ④를 반복하여 게임의 루트까지 진행함
⑥ 예시

Figure. 3. backward induction의 예시
(H, (HH, SS))가 SPE임
4. mixed strategy game [목차]
⑴ 정의 : 전략이 확률적으로 정해지는 경우
⑵ 특징 : 확률 파라미터에 따라 best response가 달라짐
⑶ 예제

Table. 6. mixed strategy game의 예제
① 조건 1. Player 1이 H와 S를 취할 확률은 각각 ω, 1-ω
② 조건 2. Player 2가 H와 S를 취할 확률은 각각 h, 1-h
③ BR(best response) : 상대방이 취할 파라미터 h 또는 ω에 대한 response임을 이해하자.
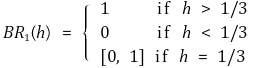
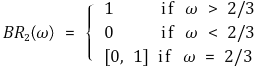
④ 내쉬균형 해는 총 세 가지가 있음
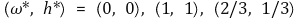
5. Bayesian game [목차]
⑴ 개요
① incomplete information : 적어도 한 플레이어가 다른 모든 플레이어의 모든 경우에 대한 페이오프를 알지 못하는 경우
② Bayesian game : incomplete information을 기반으로 한 게임
○ mixed strategy game은 action 자체에 확률이 있고, Bayesian game은 확률로 정보를 추측한다는 점에 차이가 있음
③ BNE(Bayesian Nash equilibrium) : 두 명의 플레이어에 대해 다음과 같은 전략 프로파일 (s1*(t), s2*)을 지칭함
○ 조건 1. t를 알고 있는 플레이어 1은 BR(best response)을 취해야 함
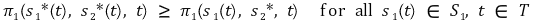
○ 조건 2. t를 모르고 있는 플레이어 2는 기댓값에 의존한 선택을 취해야 함
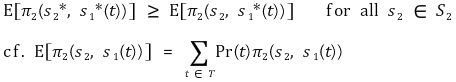
⑵ 예제
① 문제상황 : 1/3의 확률로 t = -1이고 2/3의 확률로 t = 3. t가 얼마인지는 플레이어 1만 알고 있음 (singletone)
② normal-form representation

Table. 7. Bayesian game의 normal-form representation
③ extensive form : 루트 노드를 chance node라고 함. Player 1에 대해서만 singletone이 됨을 유의

Figure. 4. Bayesian game의 extensive form
④ 전략 프로파일 : t = -1이면 H인 경우 H-1 대신 H1와 같이 표시함
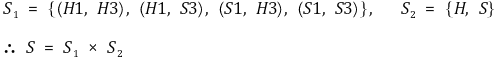
⑤ 플레이어 1의 best response 판단
○ 플레이어 1은 t = -1인 경우 무조건 S를 선택해야 함 : H1과 관련된 전략은 폐기
○ BNE 후보 : ((S1, H3), H), ((S1, H3), S), ((S1, S3), H), ((S1, S3), S)
○ ((S1, H3), H) : best response 맞음
○ ((S1, H3), S) : ((S1, S3), S)로 선택을 바꾸는 게 좋음
○ ((S1, S3), H) : ((S1, H3), H)로 선택을 바꾸는 게 좋음
○ ((S1, S3), S) : best response 맞음
⑥ 플레이어 2의 best response 판단
○ ((S1, H3), H)에 대한 판단
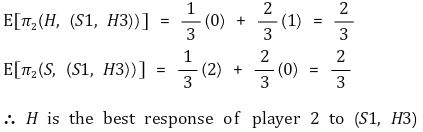
○ ((S1, S3), S)에 대한 판단
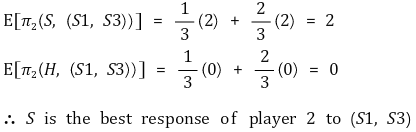
⑦ 결론 : BNE는 ((S1, H3), H), ((S1, S3), S)
6. 공약(commitment)의 경제학 [목차]
⑴ 정의 : 자신의 위협을 정말로 실천에 옮기겠다는 의지를 보이기 위해 취하는 행동
⑵ 자신에게도 손해가 올 것임을 뻔히 알면서도 위협한 대로 행동할 수밖에 없다는 점을 상대방에게 납득시키기 위함
⑶ 정책 게임 이론
입력: 2020.04.22 13:27
'▶ 사회과학 > ▷ 미시경제학' 카테고리의 다른 글
| 【미시경제학】 8강. 계약이론 (0) | 2020.05.18 |
|---|---|
| 【미시경제학】 7강. 과점시장 (0) | 2020.05.05 |
| 【미시경제학】 6강. 독점시장 (0) | 2020.04.14 |
| 【미시경제학】 5강. 완전경쟁시장 (0) | 2020.04.09 |
| 【미시경제학】 4강. 생산자 이론 (0) | 2020.03.30 |




최근댓글