통계학 기초 문제 [01-20]
추천글 : 【통계학】 통계학 목차
문제 1. a와 b가 공평한 동전을 각각 던진다. A는 a가 동전을 n+1번 던졌을 때 앞면이 나온 횟수를 나타내는 확률변수이고, B는 b가 동전을 n번 던졌을 때 앞면이 나오는 횟수를 나타내는 확률변수라고 하자. 이때 P(A > B)를 구하시오.
이 문제를 대수적으로 계산하는 것은 까다롭다.
A*를 a가 동전을 n번 던졌을 때 앞면이 나오는 횟수에 관한 확률변수라고 하자.
B*를 b가 동전을 n번 던졌을 때 앞면이 나오는 횟수에 관한 확률변수라고 하자.
P(A* > B*) = P(A* < B*)
P(A* > B*) + P(A* = B*) + P(A* < B*) = 1
P(A > B) = P(A > B | A* > B*) + P(A > B | A* = B*) + P(A > B | A* < B*)
○ P(A > B ∩ A* > B*) = 1
○ P(A > B ∩ A* = B*) = 1/2
○ P(A < B ∩ A* < B*) = 0
P(A > B) = P(A* > B*) + 1/2 P(A* = B*) = 1/2 (P(A* > B) + P(A* = B*) + P(A* < B*)) = 1/2
문제 2. 어떤 제약회사가 자사의 신약이 0.8의 확률로 기억력에 효과가 있다고 주장하고 있다. 그래서 피험자 20명을 대상으로 기억력 검사를 실시하였다. 신약이 효과가 있는 경우 항상 검사 점수가 증가한다. 신약이 효과가 없는 경우 0.5의 확률로 검사 점수가 증가하고, 0.5의 확률로 검사 점수가 감소한다. 검사 결과 20명 중 16명의 점수가 증가하였다. 기억력이 좋아지는 사건을 M, 기억력이 변화없는 사건을 N, 검사 점수가 증가하는 사건을 S, 검사 결과 20명 중 16명의 점수가 증가하는 사건을 T, 제약회사의 주장이 맞는 사건을 F1, 제약회사의 주장이 틀린 사건을 F2 이라고 정의하자. 이제 다음 각 문제를 풀어라.
⑴ 문제 2-1. P(T | F1) : 제약회사의 주장이 사실인 경우 해당 결과가 나올 확률
접근 1.

접근 2.
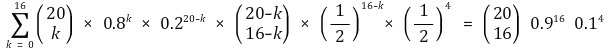
⑵ 문제 2-2. P(T | F2) : 제약회사의 주장이 틀린 경우 해당 결과가 나올 확률
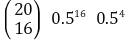
⑶ 문제 2-3. P(F1 | T) : 검사를 진행한 후 제약회사의 주장이 맞는 확률

⑷ 문제 2-4. P(M | T) : 검사를 진행한 후 제약회사의 신약으로 기억력이 좋아질 확률
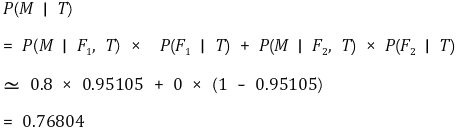
문제 3. 원점에서 시작하여 길이가 ℓ km인 해변이 존재한다. 이 해변에서 임의의 한 지점을 선택한다. 원점에서 해당 지점까지의 구간 중 임의의 한 지점을 선택한다. Y를 최초 선택 지점과 원점으로부터의 거리에 관한 확률 변수로 정의하고, X를 최종 선택 지점과 원점으로부터의 거리에 관한 확률 변수로 정의한다. 이때, p(x)를 구하여라.
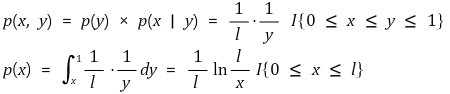
문제 4. n명의 사람들의 모자를 모두 모아 임의로 분배 시 제대로 돌려받은 사람 수에 관한 확률변수를 X라 하자. 이때, E(X), VAR(X)를 구하여라.
Xi : i번째 사람이 자신의 모자를 제대로 돌려 받으면 1, 그렇지 않으면 0이라 하자.
이제 X = X1 + ··· + Xn를 고려하자.
E(X) 계산 과정은 다음과 같다.
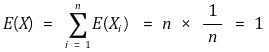
○ 핵심 : E(Xi) = 1/n
○ 해석 1. 경우의 수 접근
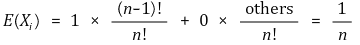
○ 해석 2. i번째 사람이 최초로 추출한 때나 그렇지 않은 때의 기댓값은 대칭성에 의해 일정
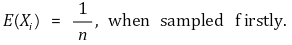
VAR(X) 계산 과정은 다음과 같다.
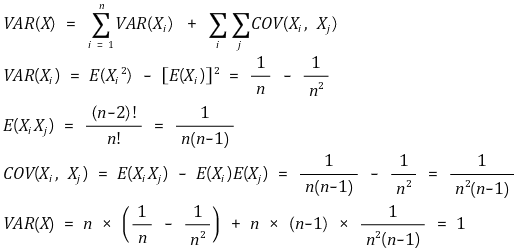
문제 5. 어떤 보험회사는 고객을 위하여 자동차를 A 회사에서 40%, B 회사에서 60%를 빌린다. A 회사와 B 회사의 고장률이 각각 10%, 5%일 때 다음에 답하여라. 이 보험회사가 자동차를 빌렸을 때 고장 날 확률을 구하여라. 또한, 자동차가 고장났을 때, 그 자동차를 B에서 빌렸을 확률을 구하여라.
이 보험회사가 자동차를 빌렸을 때 고장 날 확률 = 0.4 × 0.1 + 0.6 × 0.05 = 0.07 = 7%
자동차가 고장났을 때, 그 자동차를 B에서 빌렸을 확률 = 0.6 × 0.05 / (0.4 × 0.1 + 0.6 × 0.05) = 3/7
문제 6. 어느 공장에서 생산되는 제품 중 10%가 불량품이다. 이 공장에서 생산되는 제품 중 랜덤하게 100개를 추출하여 검사를 실시할 때 다음 확률의 근사값을 구하여라: 1) 불량품이 10개 이상일 확률, 2) 불량품이 정확히 10개일 확률. 소숫점은 셋째 자리에서 반올림하여 둘째 자리로 계산한다.
표본비율 p̂ ~ 𝒩(0.1, 0.1 × 0.9 / 100)
불량품이 10개 이상일 확률 = Pr(p̂ > 0.1 | μ = 0.1, σ = 0.03) = Pr(Z > 0) = 0.5
불량품이 정확히 10개일 확률 = 100C10·0.110·0.990 = 0.13
문제 7. 어떤 대학 입시에 응시한 학생 1000명의 수학 성적을 조사하였더니 평균이 60점, 분산이 25점인 정규분포를 보였다. 다음에 답하여라.
⑴ 문제 7-1. 수학 점수가 50점부터 70점까지 받은 학생 수
Pr(50 ≤ X ≤ 70) = Pr(-10 ≤ X - 60 ≤ 10) = Pr(-0.4 ≤ Z ≤ 0.4) = 0.3108435
N = 1000 × Pr(50 ≤ X ≤ 70) → 310명
⑵ 문제 7-2. 수학 점수가 75점을 얻은 학생은 몇 등
Pr(X ≤ 75) = Pr(X - 60 ≤ 15) = Pr(Z ≤ 0.6) = 0.7257469
M = 1000 × Pr(Z ≤ 0.6) ≒ 726등
⑶ 문제 7-3. 전체의 20%는 불합격한다면 합격의 최소 수학 점수
Pr(X ≤ k) = Pr(Z ≤ (k - 60)/25) = 0.8 = Pr(Z ≤ 0.8416212)
∴ k = 81점
문제 8. 확률변수 X, Y의 확률질량함수 P(x, y)가 다음과 같을 때, P(X = x) = P(x), E(X), V(Y), MY(t) (적률생성함수)를 구하여라.
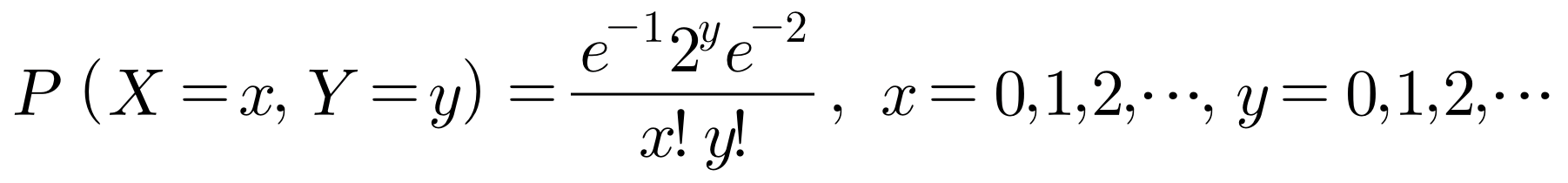
exp(x) = ∑n=0 to ∞ (xn / n!)이므로,
P(x) = (e-3 / x!)(20 / 0! + 21 / 1! + 22 / 2! + ···) = (e-3 / x!)·e2 = e-1/x!
E(X) = ∑x=1 to ∞ e-1/(x-1)! = ∑x=0 to ∞ e-1/x! = ∑all x P(x) = 1
P(y) = 2ye-2 / y!
E(Y) = 2
E(Y(Y-1)) = 4
V(Y) = E(Y2) - (E(Y))2 = E(Y(Y-1)) + E(Y) - (E(Y))2 = 4 + 2 - 4 = 2
MY(t) = E(etY) = ∑y=0 to ∞ (2yety-2 / y!) = e-2 ∑y=0 to ∞ ((2et)y / y!) = exp(-2)·exp(2et) = exp(2et - 2)
문제 9. 하나의 주사위를 두 번 던지는 실험에서 X와 Y을 각각 X = 두 번의 실험에서 나타난 홀수의 횟수, Y = 두 번의 실험에서 나타난 소수의 횟수라 하면 E(X), V(Y), X와 Y의 상관계수를 구하시오.
주사위의 눈 중 홀수는 1, 3, 5이고, 소수는 2, 3, 5이다.
E(X) = 1 × P(X = 1) + 2 × P(X = 2) = 1 × (1/2) + 2 × (1/4) = 1
E(X2) = 12 × P(X = 1) + 22 × P(X = 2) = 1 × 1/2 + 4 × 1/4 = 3/2
V(X) = E(X2) - (E(X))2 = 3/2 - 1 = 1/2
E(Y) = 1
E(Y2) = 12 × P(Y = 1) + 22 × P(Y = 2) = 1 × 1/2 + 4 × 1/4 = 3/2
V(Y) = E(Y2) - (E(Y))2 = 3/2 - 1 = 1/2
| 1번째 \ 2번째 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | ① | ③ | ③ | |||
| 2 | ① | ② | ② | |||
| 3 | ③ | ② | ④ | ① | ④ | ① |
| 4 | ① | ① | ||||
| 5 | ③ | ② | ④ | ① | ④ | ① |
| 6 | ① | ① |
E(XY) = 1 × P(X = 1, Y = 1) (①) + 2 × P(X = 1, Y = 2) (②) + 2 × P(X = 2, Y = 1) (③) + 4 × P(X = 2, Y = 2) (④)
E(XY) = 1 × 10/36 + 2 × 4/36 + 2 × 4/36 + 4 × 4/36 = 42 / 36
COV(X, Y) = E(XY) - E(X)E(Y) = 42/36 - 1 = 1/6
ρXY = COV(X, Y) / (√V(X)·√V(Y)) = (1/6) / (1/2) = 1/3
문제 10. 연속확률변수 X가 아래와 같을 때 k, P(0 < X < 1/2 | y = 3/4), P(X + Y > 1), E(X), E(X | y = 1/2), V(Y)를 구하여라.
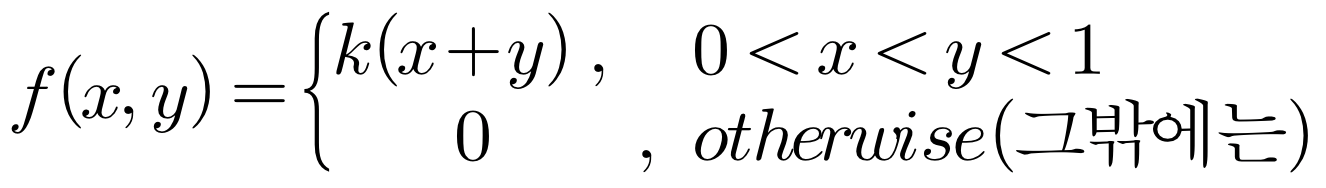
이중적분 영역을 그림을 그려서 표현하면 준 통계량을 쉽게 계산할 수 있다. (단, 여기에서는 해당 그림은 생략하도록 한다.)
1 = ∫∫ f(x, y) dxdy = k ∫0 to 1 ∫x to 1 (x + y) dydx = k/2 ⇔ k = 2
P(0 < X < 1/2 | y = 3/4) = ∫0 to 1/2 2(x + 3/4) dx / ∫0 to 3/4 2(x + 3/4) dx = 16/27
P(X + Y > 1) = ∫0.5 to 1 ∫1-y to y 2(x + y) dxdy = 2/3
E(X) = ∫0 to 1 ∫x to 1 x·2(x + y) dydx = 5/12
E(X | y = 1/2) = ∫0 to 1/2 x·2(x + 1/2) dx / ∫0 to 1/2 2(x + 1/2) dx = 5/18
E(Y) = ∫0 to 1 ∫x to 1 y·2(x + y) dydx = 3/4
E(Y2) = ∫0 to 1 ∫x to 1 y2·2(x + y) dydx = 3/5
∴ V(Y) = E(Y2) - (E(Y))2 = 3/5 - 9/16 = 3/80
문제 11. X와 Y가 E(X) = E(Y) = 1인 지수분포를 따르고 독립일 때, X + Y의 확률밀도함수를 구하라.
X ~ e-x, Y ~ e-x
X와 Y의 적률생성함수는 모두 1 / (1-t)이다.
그러므로 X + Y의 적률생성함수는 (1 / (1-t))2이고, 이는 λ = 1, r = 2인 감마분포의 적률생성함수이다.
따라서 X + Y의 확률밀도함수는 p(x; r = 2, λ = 1) = (λr / Γ(r)) · xr-1 · e-λx = xe-x
문제 12. 확률변수 X, Y의 확률밀도함수 f(x, y)가 다음과 같을 때 c, P(X + Y ≥ 1), P(X ≥ 1/2, Y ≥1/2), P(X + Y ≤ z)를 구하시오.
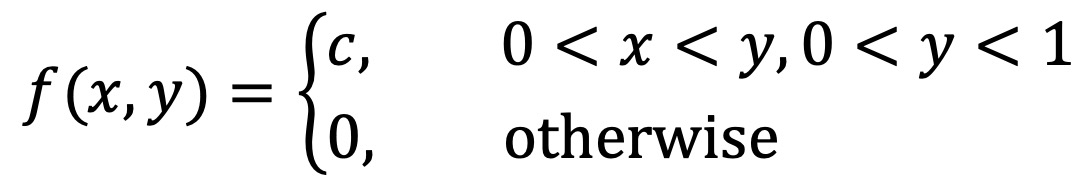
1 = ∫∫ f(x, y) dxdy = c/2 ⇔ c = 2
P(X + Y ≥ 1) = 1/2 (∵ 면적비 고려)
P(X ≥ 1/2, Y ≥ 1/2) = 1/2 (∵ 면적비 고려)
경우 1. z ≤ 0 : P(X + Y ≤ z) = 0
경우 2. 0 < z ≤ 1 : P(X + Y ≤ z) = (1/2) z2
경우 3. 1 < z ≤ 2 : P(X + Y ≤ z) = 1 - (1/2) (2-z)2
경우 4. 2 ≤ z : P(X + Y ≤ z) = 1
문제 13. P(X = x) = (1/2)x, x = 1, 2, 3, ···일 때, MX(t), V(X)를 구하여라.
MX(t) = E[etX] = ∑x=1 to ∞ (etx / 2x) = ∑x=1 to ∞ (et / 2)x = (et / 2) / (1 - (et / 2)) = -1 + 2 / (2 - et)
단, et < 2이 성립해야 수렴값이 존재함을 유의한다.
E[X] = ∂MX(t) / ∂t = 2et / (2 - et)2 at (t = 0) = 2
E[X2] = ∂2MX(t) / ∂t2 at (t = 0) = (4et + 2e2t) / (2 - et)3 at (t = 0) = 6
∴ V[X] = E[X2] - (E[X])2 = 6 - 4 = 2
문제 14. 확률변수 X, Y의 확률질량함수 P(x, y)가 P(x, y) = k(x + y), (x, y) = (1, 1), (1, 2), (2, 3)일 때 k, E(1/X), V(X)를 구하여라.
k(1 + 1) + k(1 + 2) + k(2 + 3) = 2k + 3k + 5k = 10k = 1 ⇔ k = 0.1
E(1/X) = (1/1) × 0.2 + (1/1) × 0.3 + (1/2) × 0.5 = 0.75
E(X) = 1 × 0.2 + 1 × 0.3 + 2 × 0.5 = 1.5
E(X2) = 12 × 0.2 + 12 × 0.3 + 22 × 0.5 = 2.5
∴ V(X) = E(X2) - (E(X))2 = 2.5 - 2.25 = 0.25
문제 15. 하나의 주사위를 던지는 실험에서 X와 Y를 각각 두 번의 실험에서 나타난 짝수의 횟수, 두 번의 실험에서 나타난 3의 배수의 횟수라 하면 1) X와 Y의 주변 확률분포, 2) X와 Y의 공분산과 상관계수를 구하여라.
| 1번째 \ 2번째 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | X=0, Y=0 | X=1, Y=0 | X=0, Y=1 | X=1, Y=0 | X=0, Y=0 | X=1, Y=1 |
| 2 | X=1, Y=0 | X=2, Y=0 | X=1, Y=1 | X=2, Y=0 | X=1, Y=0 | X=2, Y=1 |
| 3 | X=0, Y=1 | X=1, Y=1 | X=0, Y=2 | X=1, Y=1 | X=0, Y=1 | X=1, Y=2 |
| 4 | X=1, Y=0 | X=2, Y=0 | X=1, Y=1 | X=2, Y=0 | X=1, Y=0 | X=2, Y=1 |
| 5 | X=0, Y=0 | X=1, Y=0 | X=0, Y=1 | X=1, Y=0 | X=0, Y=0 | X=1, Y=1 |
| 6 | X=1, Y=1 | X=2, Y=1 | X=1, Y=2 | X=2, Y=1 | X=1, Y=1 | X=2, Y=2 |
PX(x) = 9/36 (X = 0), 18/36 (X = 1), 9/36 (X = 2)
PY(y) = 16/36 (Y = 0), 16/36 (Y = 1), 4/36 (Y = 2)
E[X] = 1
E[Y] = 2/3
E[XY] = 1 × 1 × 8/36 + 1 × 2 × 2/36 + 2 × 1 × 4/36 + 2 × 2 × 1/36 = 2/3
COV(X, Y) = E[XY] - E[X]·E[Y] = 2/3 - 2/3 = 0
따라서 상관계수 또한 0
문제 16. 확률변수 X와 Y는 독립이고, 적률생성함수(M.G.F.)가 각각 MX(t) = exp(2et - 2), MY(t) = (1/4)10(3et + 1)10일 때, P(X + Y = 2), E[XY]를 구하시오.
푸아송 분포 P(X = x | λ) = e-λ λx / x!의 적률생성함수는 MX(t) = exp(λet - λ)임을 상기하자.
또한, 이항분포 P(X = x) = nCx θx (1 - θ)n-x의 적률생성함수는 MX(t) = (θet + 1 - θ)n임을 상기하자.
그러므로, P(X = x) = e-2 2x / x!이고 P(Y = y) = 10Cy (3/4)y (1/4)10-y이다.
따라서, P(X + Y = 2) = P(X = 2, Y = 0) + P(X = 1, Y = 1) + P(X = 0, Y = 2) = (1/4)10 × 467 / e2
또한, X와 Y는 독립이므로, E[XY] = E[X] × E[Y] = 2 × (10 × 3/4) = 15
문제 17. 확률변수 X가 정규분포 N(m, σ2)일 때, E[X], V[X], MX(t)를 구하여라.
문제 18. 어떤 부품의 수명에 대한 결합확률분포가 다음과 같을 때 1) P(X > 1 | Y > 1), 2) X와 Y는 독립인지, 3) σX, 4) Corr(X, Y)를 구하여라.
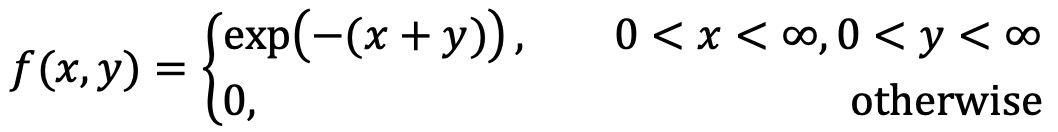
f(x, y) = exp(-x) × exp(-y) = fX(x) × fY(y)이므로 X와 Y는 독립
P(X > 1 | Y > 1) = P(X > 1) (∵ X와 Y는 독립) = ∫1 to ∞ exp(-x) dx = e-1
E[X] = ∫0 to ∞ x exp(-x) dx = 1
E[X2] = ∫0 to ∞ x2 exp(-x) dx = 2
∴ σX = √V[X] = √(E[X2] - (E[X])2) = √(2 - 1) = 1
Corr(X, Y) = 0 (∵ X와 Y는 독립)
문제 19. 이산확률변수 X와 Y의 결합확률질량함수(p.n.f)가 다음과 같을 때, P(X ≤ 1), MX(t), V[X]를 구하여라.
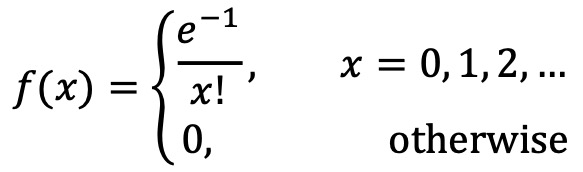
문제 20. 이산확률변수 X의 확률질량함수 f(x) = (1/2)x, x = 1, 2, 3, ···일 때, MX(t), E[2X - 3], V[2X - 3]을 구하여라.
MX(t) = E[etX] = ∑x=1 to ∞ (et / 2)x = (et / 2) / [1 - (et / 2)] = et / (2 - et)
E[X] = ∂/∂t MX(t) |t=0 = 2et / (2 - et)2 |t=0 = 2
E[X2] = ∂2/∂t2 MX(t) |t=0 = (4et + 2e2t) / (2 - et)3 |t=0 = 6
E[2X - 3] = 2E[X] - 3 = 1
V[2X - 3] = 4V[X] = 4(E[X2] - (E[X])2) = 4(6 - 4) = 8
입력: 2019.07.04 10:13
수정: 2024.12.24 16:59
'▶ 자연과학 > ▷ 조합론·통계학' 카테고리의 다른 글
| 【통계학】 통계학 기초 문제 [41-60] (6) | 2024.12.26 |
|---|---|
| 【통계학】 통계학 기초 문제 [21-40] (2) | 2024.12.25 |
| 【통계학】 14-8강. Cochran-Mantel-Haenszel (CMH) 검정 (7) | 2024.10.14 |
| 【통계학】 18강. 회귀분석의 정규화 (2) | 2024.10.10 |
| 【통계학】 21강. 정보이론 (5) | 2024.10.07 |
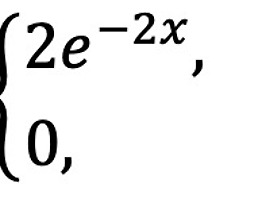



최근댓글