가설을 생성하는 AI, 그 아이디어의 시작
추천글 : 【철학】 인공지능 철학 목차
a. 수학 논리 문제
c. 수학 문제를 푸는 AI
길을 물어물어 찾아가듯 탐구라는 것은 하나의 질문을 던지고 그에 답하고 다음 질문을 발견하여 다시 답하는, 하나로 이어지는 과정과 같다. - Max Perutz
최근 나는 취리히 공과대학에서 파이널 면접을 치렀다. 지금부터 최종 합격률은 50% 정도 되는 것 같다. 공간전사체를 넘어선 시공간전사체라는 기술이 눈 앞에 있었고, 그들은 나에게 어떻게 이 데이터를 어떻게 해석할지 좋은지 질문했다. 그때 내 머릿속에서는 '가설 생성형 AI' (hypothesis-generating AI)라는 키워드가 떠올랐다. 너무나 반응이 뜨거웠던, 하지만 조금 한편으로는 그들에게는 esoteric 했을 것 같고 나조차도 버거워하는 주제였다.
사실 데이터를 통해 가설을 생성하는 것은 2년 넘게 재직한 회사에서 얻은 통찰이었다. 신약 개발은 때로는 10년 넘게 이어지는 마라톤이고 최종 단계에 와서 뜻하지 않은 임상 시험 결과를 맞이하면서 실패하는 경우가 많다. 따라서, 임상 시험 결과를 바탕으로 역으로 가설을 만들면서 스토리텔링을 구축하는 스마트한 전략의 신약 개발을 시도하는 회사였다. 그래서 데이터로부터 가설을 만드는 접근은 나에게 전혀 어색하지 않았고, 거기에 한술 더 떠 ChatGPT의 시대에 AI가 가설을 만들 수도 있다고 생각했다.
내가 '가설 생성형 AI'라는 아이디어가 어디에서 왔는지 곱씹어 봤을 때, "Beyond RG: from parameter flow to metric flow" (Strandkvist, C. et al)라는 논문에서 시작했던 것 같다. 고차원의(high-dimensional) 파라미터로부터 이론을 생성하는, 어렵지만 상당히 재미있는 수학 이론이었다.

Figure. 1. 기본 용어

Figure. 2. 관심 질문(question of interest)을 수학적으로 표현
이 논문을 곱씹어 보자니, 데이터의 차원이 증가하여 해석가능성이 떨어지고, 이로 인해 가설 생성형 AI를 만들어야 한다는 나의 계획은 어쩌면 허무맹랑한 이야기는 아니고 정말로 실행 가능한 미래라는 확신이 생겼다. 그래서 정말로 가설을 세우고 여러 가지를 테스트해보면서 정말로 유효 적절한 가설을 찾아가는 머신러닝 알고리즘을 실험 삼아 개발해 보았다.
현재 주목하고 있는 구체적인 문제는 다음과 같다.
"크기와 모양이 같은 6개의 구슬이 있다. 이 중에서 3개는 무겁고, 나머지 3개는 가볍다. 단, 무거운 3개의 무게는 서로 같고, 가벼운 3개의 무게는 서로 같다. 이때, 양팔저울을 3번 써서 구슬을 무거운 것과 가벼운 것으로 구별하여라."
우선 다음과 같은 고려사항이 있었다.
○ 머신러닝 코드는 전략을 생성하는 파트와 전략을 검증하는 파트로 구분된다.
○ 양팔저울을 사용하여 비교하는 방식은 항상 3개 vs 3개, 2개 vs 2개, 1개 vs 1개와 같이 진행된다. 왜냐하면 그 이외의 경우에는 유효한 정보를 얻기 어렵기 때문이다. 양팔저울을 비교함으로써 얻게 되는 '정보'를 어떻게 정의하면 좋을지 고민이 많았다. 사실 확률론이나 대수적으로 그러한 '정보'를 정의하는 게 가능할 수도 있겠다는 생각을 했다. (ref) 하지만, 현재 필자의 역량으로는 한계가 있으며 언제나 조합론적 사고를 우선하는 입장에서, 양팔저울을 비교함으로써 '경우의 수를 좁힐 수 있다'는 필요충분적인 조건을 얻을 수 있음을 포착하고 적극 활용하기로 했다.
○ 어떤 전략과 양팔저울 비교 결과가 주어졌을 때, 가능한 heavy set의 조합을 potential heavy set(s)으로 정의하였다. 이때, potential heavy set(s)이 1개인 경우뿐만 아니라 0개인 경우도 유효하다고 보았는데, 왜냐하면 주어진 정보가 아얘 터무니 없어서 정말로 유효하게 설정한 전략을 기각하는 일을 피해야 했기 때문이다.
자, 이제 전략을 생성하는 코드, 전략을 검증하는 코드를 여러 시행착오를 통해 완성하고자 한다.
⑴ 3 vs 3 (1, 2, 3) > (4, 5, 6), (1, 2, 4) > (3, 5, 6), (1, 2, 5) > (3, 4, 6)과 같은 정보가 주어져 있을 때 potential heavy set(s)을 출력
from itertools import combinations
def get_potential_heavy_sets(weighing1, weighing2, weighing3):
# Initial beads
beads = [1, 2, 3, 4, 5, 6]
potential_heavy_sets1 = [combo for combo in combinations(beads, 3) if len(set(combo) & set(weighing1)) >= 2]
potential_heavy_sets2 = [combo for combo in combinations(beads, 3) if len(set(combo) & set(weighing2)) >= 2]
potential_heavy_sets3 = [combo for combo in combinations(beads, 3) if len(set(combo) & set(weighing3)) >= 2]
# Intersect the three potential heavy sets
final_potential_heavy_sets = list(set(potential_heavy_sets1) & set(potential_heavy_sets2) & set(potential_heavy_sets3))
return final_potential_heavy_sets
weighing1 = (1, 2, 3) # Beads in the left pan during the first weighing
weighing2 = (1, 2, 4) # Beads in the left pan during the second weighing
weighing3 = (1, 2, 5) # Beads in the left pan during the third weighing
print("Possible sets of heavy beads:", get_potential_heavy_sets(weighing1, weighing2, weighing3))
⑵ 3 vs 3 (1, 2, 3) vs (4, 5, 6), (1, 2, 4) vs (3, 5, 6), (1, 2, 5) vs (3, 4, 6) 전략일 때 각 potential heavy set(s)을 출력
from itertools import combinations
def potential_sets_for_weighing(weighing, beads, is_heavier):
if is_heavier:
return [combo for combo in combinations(beads, 3) if len(set(combo) & set(weighing)) >= 2]
else:
return [combo for combo in combinations(beads, 3) if len(set(combo) - set(weighing)) >= 2]
def get_all_potential_heavy_sets(weighing1, weighing2, weighing3):
beads = [1, 2, 3, 4, 5, 6]
results = []
for state1 in [True, False]: # True = heavier, False = lighter
for state2 in [True, False]:
for state3 in [True, False]:
potential_sets1 = potential_sets_for_weighing(weighing1, beads, state1)
potential_sets2 = potential_sets_for_weighing(weighing2, beads, state2)
potential_sets3 = potential_sets_for_weighing(weighing3, beads, state3)
intersected_sets = list(set(potential_sets1) & set(potential_sets2) & set(potential_sets3))
if intersected_sets:
results.append({
"states": (state1, state2, state3),
"sets": intersected_sets
})
return results
weighing1 = (1, 2, 3)
weighing2 = (1, 2, 4)
weighing3 = (1, 2, 5)
all_results = get_all_potential_heavy_sets(weighing1, weighing2, weighing3)
for result in all_results:
states_str = ["heavier" if s else "lighter" for s in result["states"]]
print(f"When weighing1 is {states_str[0]}, weighing2 is {states_str[1]}, and weighing3 is {states_str[2]}:")
print("Possible sets of heavy beads:", result["sets"])
print("----")
⑶ 3 vs 3 (1, 2, 3) vs (4, 5, 6), (1, 2, 4) vs (3, 5, 6), (1, 2, 5) vs (3, 4, 6) 전략일 때 항상 0-1개의 potential heavy set(s)을 출력하는지
from itertools import combinations
def potential_sets_for_weighing(weighing, beads, is_heavier):
if is_heavier:
return [combo for combo in combinations(beads, 3) if len(set(combo) & set(weighing)) >= 2]
else:
return [combo for combo in combinations(beads, 3) if len(set(combo) - set(weighing)) >= 2]
def get_all_potential_heavy_sets(weighing1, weighing2, weighing3):
beads = [1, 2, 3, 4, 5, 6]
results = []
for state1 in [True, False]: # True = heavier, False = lighter
for state2 in [True, False]:
for state3 in [True, False]:
potential_sets1 = potential_sets_for_weighing(weighing1, beads, state1)
potential_sets2 = potential_sets_for_weighing(weighing2, beads, state2)
potential_sets3 = potential_sets_for_weighing(weighing3, beads, state3)
intersected_sets = list(set(potential_sets1) & set(potential_sets2) & set(potential_sets3))
if intersected_sets:
results.append(len(intersected_sets) <= 1) # Store True if there's only one potential heavy set
return all(results) # Returns True if all strategies result in a unique potential heavy set
weighing1 = (1, 2, 3)
weighing2 = (1, 2, 4)
weighing3 = (1, 2, 5)
result = get_all_potential_heavy_sets(weighing1, weighing2, weighing3)
if result:
print("All cases always output only one potential heavy set.")
else:
print("There exists a case that does not output a unique potential heavy set.")
⑷ 3 vs 3 결론 1. 3개 vs 3개 비교를 세 번 수행했을 때, 모든 경우에서 유효한 전략이 있는지 : 없음
from itertools import combinations
def potential_sets_for_weighing(weighing, beads, is_heavier):
if is_heavier:
return [combo for combo in combinations(beads, 3) if len(set(combo) & set(weighing)) >= 2]
else:
return [combo for combo in combinations(beads, 3) if len(set(combo) - set(weighing)) >= 2]
def get_all_potential_heavy_sets(weighing1, weighing2, weighing3):
beads = [1, 2, 3, 4, 5, 6]
results = []
for state1 in [True, False]: # True = heavier, False = lighter
for state2 in [True, False]:
for state3 in [True, False]:
potential_sets1 = potential_sets_for_weighing(weighing1, beads, state1)
potential_sets2 = potential_sets_for_weighing(weighing2, beads, state2)
potential_sets3 = potential_sets_for_weighing(weighing3, beads, state3)
intersected_sets = list(set(potential_sets1) & set(potential_sets2) & set(potential_sets3))
if intersected_sets:
results.append(len(intersected_sets) <= 1) # Store True if there's only one potential heavy set
return all(results) # Returns True if all strategies result in a unique potential heavy set
beads = [1, 2, 3, 4, 5, 6]
successful_combinations = []
for weighing1 in combinations(beads, 3):
for weighing2 in combinations(beads, 3):
for weighing3 in combinations(beads, 3):
result = get_all_potential_heavy_sets(weighing1, weighing2, weighing3)
if result:
successful_combinations.append((weighing1, weighing2, weighing3))
print("Combinations of (weighing1, weighing2, weighing3) that always output only one potential heavy set:")
for combo in successful_combinations:
print(combo)
⑸ 2 vs 2 (1, 2) > (4, 5), (1, 2) > (3, 5), (1, 2) > (3, 4)과 같은 정보가 주어져 있을 때 potential heavy set(s)을 출력
from itertools import combinations
def get_potential_heavy_sets_for_2_vs_2(weighing1_1, weighing1_2, weighing2_1, weighing2_2, weighing3_1, weighing3_2):
beads = [1, 2, 3, 4, 5, 6]
# Identify potential heavy sets for each weighing
potential_heavy_sets1 = []
for comb in combinations(beads, 3):
if len( set(weighing1_1) & set(comb) ) > len( set(weighing1_2) & set(comb) ):
potential_heavy_sets1.append(comb)
potential_heavy_sets2 = []
for comb in combinations(beads, 3):
if len( set(weighing2_1) & set(comb) ) > len( set(weighing2_2) & set(comb) ):
potential_heavy_sets2.append(comb)
potential_heavy_sets3 = []
for comb in combinations(beads, 3):
if len( set(weighing3_1) & set(comb) ) > len( set(weighing3_2) & set(comb) ):
potential_heavy_sets3.append(comb)
# Intersect the potential heavy sets to identify common sets
final_potential_heavy_sets = list(set(potential_heavy_sets1) & set(potential_heavy_sets2) & set(potential_heavy_sets3))
return final_potential_heavy_sets
weighing1_1 = (1, 2) # Beads in the left pan during the first weighing
weighing1_2 = (4, 5) # Beads in the right pan during the first weighing
weighing2_1 = (1, 2) # Beads in the left pan during the second weighing
weighing2_2 = (3, 5) # Beads in the right pan during the second weighing
weighing3_1 = (1, 2) # Beads in the left pan during the third weighing
weighing3_2 = (3, 4) # Beads in the right pan during the third weighing
print("Possible sets of heavy beads:", get_potential_heavy_sets_for_2_vs_2(weighing1_1, weighing1_2, weighing2_1, weighing2_2, weighing3_1, weighing3_2))
⑹ 2 vs 2 (1, 2) vs (4, 5), (1, 2) vs (3, 5), (1, 2) vs (3, 4) 전략일 때 각 potential heavy set(s)을 출력
from itertools import combinations, product
def get_potential_heavy_sets_for_2_vs_2(weighing1_1, weighing1_2, weighing2_1, weighing2_2, weighing3_1, weighing3_2):
beads = [1, 2, 3, 4, 5, 6]
scenarios = {
">": lambda w1, w2, comb: len(set(w1) & set(comb)) > len(set(w2) & set(comb)),
"<": lambda w1, w2, comb: len(set(w1) & set(comb)) < len(set(w2) & set(comb)),
"=": lambda w1, w2, comb: len(set(w1) & set(comb)) == len(set(w2) & set(comb))
}
results = {}
for outcome1, outcome2, outcome3 in product(scenarios.keys(), repeat=3):
potential_heavy_sets1 = [comb for comb in combinations(beads, 3) if scenarios[outcome1](weighing1_1, weighing1_2, comb)]
potential_heavy_sets2 = [comb for comb in combinations(beads, 3) if scenarios[outcome2](weighing2_1, weighing2_2, comb)]
potential_heavy_sets3 = [comb for comb in combinations(beads, 3) if scenarios[outcome3](weighing3_1, weighing3_2, comb)]
intersected_sets = list(set(potential_heavy_sets1) & set(potential_heavy_sets2) & set(potential_heavy_sets3))
results[(outcome1, outcome2, outcome3)] = intersected_sets
return results
weighing1_1 = (1, 2)
weighing1_2 = (4, 5)
weighing2_1 = (1, 2)
weighing2_2 = (3, 5)
weighing3_1 = (1, 2)
weighing3_2 = (3, 4)
all_results = get_potential_heavy_sets_for_2_vs_2(weighing1_1, weighing1_2, weighing2_1, weighing2_2, weighing3_1, weighing3_2)
for outcome, heavy_sets in all_results.items():
print(f"Outcome {outcome}: {heavy_sets}")
⑺ 2 vs 2 (1, 2) > (4, 5), (1, 2) > (3, 5), (1, 2) > (3, 4) 전략일 때 항상 0-1개의 potential heavy set(s)을 출력하는지
from itertools import combinations, product
def get_potential_heavy_sets_for_2_vs_2(weighing1_1, weighing1_2, weighing2_1, weighing2_2, weighing3_1, weighing3_2):
beads = [1, 2, 3, 4, 5, 6]
scenarios = {
">": lambda w1, w2, comb: len(set(w1) & set(comb)) > len(set(w2) & set(comb)),
"<": lambda w1, w2, comb: len(set(w1) & set(comb)) < len(set(w2) & set(comb)),
"=": lambda w1, w2, comb: len(set(w1) & set(comb)) == len(set(w2) & set(comb))
}
results = {}
always_0_or_1 = True
for outcome1, outcome2, outcome3 in product(scenarios.keys(), repeat=3):
potential_heavy_sets1 = [comb for comb in combinations(beads, 3) if scenarios[outcome1](weighing1_1, weighing1_2, comb)]
potential_heavy_sets2 = [comb for comb in combinations(beads, 3) if scenarios[outcome2](weighing2_1, weighing2_2, comb)]
potential_heavy_sets3 = [comb for comb in combinations(beads, 3) if scenarios[outcome3](weighing3_1, weighing3_2, comb)]
intersected_sets = list(set(potential_heavy_sets1) & set(potential_heavy_sets2) & set(potential_heavy_sets3))
# Check if the length of intersected_sets is not 0 or 1
if len(intersected_sets) not in [0, 1]:
always_0_or_1 = False
results[(outcome1, outcome2, outcome3)] = intersected_sets
return always_0_or_1
weighing1_1 = (1, 2)
weighing1_2 = (4, 5)
weighing2_1 = (1, 2)
weighing2_2 = (3, 5)
weighing3_1 = (1, 2)
weighing3_2 = (3, 4)
check_condition = get_potential_heavy_sets_for_2_vs_2(weighing1_1, weighing1_2, weighing2_1, weighing2_2, weighing3_1, weighing3_2)
if check_condition:
print("The strategy always outputs 0 or 1 potential heavy sets for each scenario.")
else:
print("The strategy doesn't always output 0 or 1 potential heavy sets for each scenario.")
⑻ 2 vs 2 결론 2. 2개 vs 2개 비교를 세 번 수행했을 때, 모든 경우에서 유효한 전략이 있는지 : 없음
from itertools import combinations, product
def get_potential_heavy_sets_for_2_vs_2(weighing1_1, weighing1_2, weighing2_1, weighing2_2, weighing3_1, weighing3_2):
beads = [1, 2, 3, 4, 5, 6]
scenarios = {
">": lambda w1, w2, comb: len(set(w1) & set(comb)) > len(set(w2) & set(comb)),
"<": lambda w1, w2, comb: len(set(w1) & set(comb)) < len(set(w2) & set(comb)),
"=": lambda w1, w2, comb: len(set(w1) & set(comb)) == len(set(w2) & set(comb))
}
for outcome1, outcome2, outcome3 in product(scenarios.keys(), repeat=3):
potential_heavy_sets1 = [comb for comb in combinations(beads, 3) if scenarios[outcome1](weighing1_1, weighing1_2, comb)]
potential_heavy_sets2 = [comb for comb in combinations(beads, 3) if scenarios[outcome2](weighing2_1, weighing2_2, comb)]
potential_heavy_sets3 = [comb for comb in combinations(beads, 3) if scenarios[outcome3](weighing3_1, weighing3_2, comb)]
intersected_sets = list(set(potential_heavy_sets1) & set(potential_heavy_sets2) & set(potential_heavy_sets3))
# Return False if the length of intersected_sets is not 0 or 1
if len(intersected_sets) not in [0, 1]:
return False
return True
all_2_combinations = list(combinations([1, 2, 3, 4, 5, 6], 2))
# Filter combinations to ensure the two beads do not have any intersection.
filtered_combinations = [(a, b) for a, b in product(all_2_combinations, repeat=2) if len(set(a) & set(b)) == 0]
valid_weighings = []
# Use itertools.product to replace nested loops
for weighing1, weighing2, weighing3 in product(filtered_combinations, repeat=3):
if get_potential_heavy_sets_for_2_vs_2(*weighing1, *weighing2, *weighing3):
valid_weighings.append((weighing1, weighing2, weighing3))
for weigh in valid_weighings:
print(weigh)
⑼ (1, 2, 3) vs (1, 2, 3) 결론 3. 임의의 양팔저울 비교를 세 번 수행했을 때, 모든 경우에서 유효한 전략이 있는지 검증 : 없음
from itertools import combinations, product
beads = [1, 2, 3, 4, 5, 6]
# Part 1: Refactor existing methods
# 3 vs 3
scenarios_3v3 = {
">": True, # Left is heavier
"<": False # Right is heavier
}
def potential_heavy_3v3(weighing1, weighing2, outcome):
is_heavier = scenarios_3v3[outcome]
if is_heavier:
return [combo for combo in combinations(beads, 3) if len(set(combo) & set(weighing1)) >= 2]
else:
return [combo for combo in combinations(beads, 3) if len(set(combo) & set(weighing2)) >= 2]
# 2 vs 2
scenarios_2v2 = {
">": lambda w1, w2, comb: len(set(w1) & set(comb)) > len(set(w2) & set(comb)),
"<": lambda w1, w2, comb: len(set(w1) & set(comb)) < len(set(w2) & set(comb)),
"=": lambda w1, w2, comb: len(set(w1) & set(comb)) == len(set(w2) & set(comb))
}
def potential_heavy_2v2(weighing1, weighing2, outcome):
return [comb for comb in combinations(beads, 3) if scenarios_2v2[outcome](weighing1, weighing2, comb)]
# 1 vs 1
scenarios_1v1 = {
">": lambda w1, w2, comb: w1 in comb and w2 not in comb, # w1 is potentially heavier
"<": lambda w1, w2, comb: w2 in comb and w1 not in comb, # w2 is potentially heavier
"=": lambda w1, w2, comb: w1 in comb and w2 in comb or w1 not in comb and w2 not in comb
}
def potential_heavy_1v1(weighing1, weighing2, outcome):
# If the weighings are individual beads, wrap them in a tuple
weighing1 = (weighing1,) if isinstance(weighing1, int) else weighing1
weighing2 = (weighing2,) if isinstance(weighing2, int) else weighing2
return [comb for comb in combinations(beads, 3) if scenarios_1v1[outcome](weighing1[0], weighing2[0], comb)]
# Part 2: Combined method
def find_valid_weighings():
valid_weighings = []
# Weighing strategies
weighings = {
3: list(combinations(beads, 3)),
2: list(combinations(beads, 2)),
1: beads
}
weighing_functions = {
3: potential_heavy_3v3,
2: potential_heavy_2v2,
1: potential_heavy_1v1
}
for size1 in [3, 2, 1]:
for weighing1_left in weighings[size1]:
for weighing1_right in weighings[size1]:
if weighing1_left == weighing1_right:
continue
for size2 in [3, 2, 1]:
for weighing2_left in weighings[size2]:
for weighing2_right in weighings[size2]:
if weighing2_left == weighing2_right:
continue
for size3 in [3, 2, 1]:
for weighing3_left in weighings[size3]:
for weighing3_right in weighings[size3]:
if weighing3_left == weighing3_right:
continue
if isinstance(weighing1_left, int):
weighing1_left = (weighing1_left,)
if isinstance(weighing1_right, int):
weighing1_right = (weighing1_right,)
if isinstance(weighing2_left, int):
weighing2_left = (weighing2_left,)
if isinstance(weighing2_right, int):
weighing2_right = (weighing2_right,)
if isinstance(weighing3_left, int):
weighing3_left = (weighing3_left,)
if isinstance(weighing3_right, int):
weighing3_right = (weighing3_right,)
if set(weighing1_left) & set(weighing1_right):
continue
if set(weighing2_left) & set(weighing2_right):
continue
if set(weighing3_left) & set(weighing3_right):
continue
results = []
for outcome1 in (scenarios_2v2 if size1 == 2 else (scenarios_1v1 if size1 == 1 else scenarios_3v3)):
for outcome2 in (scenarios_2v2 if size2 == 2 else (scenarios_1v1 if size2 == 1 else scenarios_3v3)):
for outcome3 in (scenarios_2v2 if size3 == 2 else (scenarios_1v1 if size3 == 1 else scenarios_3v3)):
potential1 = weighing_functions[size1](weighing1_left, weighing1_right, outcome1)
potential2 = weighing_functions[size2](weighing2_left, weighing2_right, outcome2)
potential3 = weighing_functions[size3](weighing3_left, weighing3_right, outcome3)
intersected_sets = list(set(potential1) & set(potential2) & set(potential3))
results.append(len(intersected_sets) <= 1) # clearly identify which one is heavy or unrealistic
if all(results):
valid_weighings.append(((weighing1_left, weighing1_right),
(weighing2_left, weighing2_right),
(weighing3_left, weighing3_right)))
print(valid_weighings)
return valid_weighings
# Part 3: Execute the combined method
valid_weighings = find_valid_weighings()
# Print the results
print("Valid combinations:")
for weigh in valid_weighings:
print(weigh)
답을 찾지 못해 여러 케이스들을 하나하나 검토해 보았더니 중요한 통찰을 얻을 수 있었다. 사실 위와 같이 동시게임(simultaneous game)으로 풀이를 구성하면 안 되고, 순차게임(sequential game)으로 풀이를 구성해야 한다는 것이다. 예를 들어, 답은 다음과 같으며, 코드를 더 발전시키지 않은 것은 순전히 필자의 변덕 때문이다.
정답
⑴ 주어진 6개의 공에 1번부터 6번까지 번호를 매긴다.
⑵ 1단계. (1, 2)와 (3, 4)를 비교한다.
⑶ 경우 1. (1, 2) > (3, 4)
① 무거운 공의 조합
○ (1, 2, 3)
○ (1, 2, 4)
○ (1, 2, 5)
○ (1, 2, 6)
○ (1, 5, 6)
○ (2, 5, 6)
② 2단계. 3번과 6번 공을 비교
③ 3단계. 2단계의 결과에 따라 다음과 같이 다른 전략을 사용한다.
○ 3번 > 6번 : 추가로 할 것 없이 (1, 2, 3)으로 결정됨
○ 3번 = 6번 : 4번 공과 5번 공을 비교하여 (1, 2, 4), (1, 2, 5) 중 유일하게 결정할 수 있음
○ 3번 < 6번 : 1번 공과 2번 공을 비교하여 (1, 2, 6), (1, 5, 6), (2, 5, 6) 중 유일하게 결정할 수 있음
⑷ 경우 2. (1, 2) = (3, 4)
① 무거운 공의 조합
○ (1, 3, 5)
○ (1, 3, 6)
○ (1, 4, 5)
○ (1, 4, 6)
○ (2, 3, 5)
○ (2, 3, 6)
○ (2, 4, 5)
○ (2, 4, 6)
② 2단계. (1, 3)과 (2, 5)를 비교한다.
③ 3단계. 2단계의 결과에 따라 다음과 같이 다른 전략을 사용한다.
○ (1, 3) > (2, 5) : 4번 공과 5번 공을 비교하여 (1, 3, 5), (1, 3, 6), (1, 4, 6) 중 유일하게 결정할 수 있음
○ (1, 3) = (2, 5) : 1번 공과 2번 공을 비교하여 (1, 4, 5), (2, 3, 6) 중 유일하게 결정할 수 있음
○ (1, 3) < (2, 5) : 3번 공과 6번 공을 비교하여 (2, 3, 5), (2, 4, 5), (2, 4, 6) 중 유일하게 결정할 수 있음
오답. 3 vs 3으로 시작하는 경우 : 1단계에서 경우의 수가 10으로 줄어들고, 2단계에서 3, 3, 4로 쪼개는데 이때 4 부분을 3단계에서 결정할 수 없음
⑴ 주어진 6개의 공에 1번부터 6번까지 번호를 매긴다.
⑵ 1단계. (1, 2, 3)과 (4, 5, 6)을 비교한다. 대칭성에 의해 (1, 2, 3) < (4, 5, 6)이라고 할 수 있다. 이 경우 무거운 공의 조합은 다음과 같다.
① (1, 4, 5)
② (1, 4, 6)
③ (1, 5, 6)
④ (2, 4, 5)
⑤ (2, 4, 6)
⑥ (2, 5, 6)
⑦ (3, 4, 5)
⑧ (3, 4, 6)
⑨ (3, 5, 6)
⑩ (4, 5, 6)
⑶ 2단계. (1, 4)와 (2, 5)를 비교한다.
⑷ 3단계. 2단계의 결과에 따라 다음과 같이 다른 전략을 사용한다.
① (1, 4) > (2, 5)인 경우 : 무거운 공의 조합은 (1, 4, 5), (1, 4, 6), (3, 4, 6) 밖에 없으므로 3번과 5번 공을 비교한다.
○ 3 > 5 : (3, 4, 6)이 무거운 공
○ 3 = 5 : (1, 4, 6)이 무거운 공
○ 3 < 5 : (1, 4, 5)이 무거운 공
② (1, 4) < (2, 5)인 경우 : 무거운 공의 조합은 (2, 4, 5), (2, 5, 6), (3, 5, 6) 밖에 없으므로 3번과 4번 공을 비교한다.
○ 3 > 4 : (3, 5, 6)이 무거운 공
○ 3 = 4 : (2, 5, 6)이 무거운 공
○ 3 < 4 : (2, 4, 5)가 무거운 공
③ (1, 4) = (2, 5)인 경우 : 무거운 공의 조합은 (2, 4, 6), (3, 4, 5), (1, 5, 6), (4, 5, 6)가 있으므로 비둘기 집의 원리에 의해 1번의 비교로 이들을 유일하게 결정할 수 없다. (실패)
위와 같은 코드들은 ChatGPT 4.0에 쉬운 케이스부터 일반화(cf. low-dimension → high-dimension)를 거듭하여 완성한 것이다. 심지어 이러한 히스토리만을 ChatGPT에게 제공해도 비슷한 유형의 문제가 있을 때 비슷한 trials-and-errors를 거쳐 최종 문제 풀이 전략을 설정해 가는 것이 가능할 것이라고 전망한다. 마치 ChatGPT와 같은 LLM 여러 개로 이루어진 cascaded control circuit이 가설(전략)을 생성하는 AI가 될 수 있다는 듯이.

7대 수학 난제 중 하나인 P대 NP 문제의 함의는 '수학 문제를 푸는 것을 일반화하는 것' 또한 수학 문제가 될 수 있다는 것이다. ChatGPT의 압도적인 퍼포먼스와 프롬프트 엔지니어링이 있는 지금, 수학 문제를 푸는 일반적인 방법론(즉, 적절한 open/closed serial/parallel control circuit)을 구축할 수 있다면 hypothesis-generating AI, strategy-generating AI의 구현이 멀지는 않았을 것이다. 그러한 일반적인 방법론을 구축하려면 우리의 모든 집단지성이 어떻게 정리돼 왔는지 이해할 것이 요구되고, 그것이 필자가 앞으로 가고자 하는 길과 맞닿아 있다.
다만, 위 풀이의 단점은 모든 경우의 수에 집착한다는 점이다. AlphaGo는 바둑이라는 앞도적으로 많은 경우의 수를 다음 수를 착수하는 것의 패턴으로 극복했고, AlphaFold2나 RFDiffusion은 biophysics background knowledge를 바탕으로 model complexity를 크게 줄여 퍼포먼스가 높은 AI를 만들 수 있었다. 더 스마트하게 가설을 생성하려면, 모든 경우의 수에 집착하지 않는 방법을 초기 단계부터 제시해야 할 것으로 보인다.
이 글을 쓰고 불과 2달쯤 지난 12월 14일 네이처 본지에 Google DeepMind 논문이 하나 발표됐다. 단순히 기존 지식과의 pattern-matching을 하는 것을 넘어, LLM을 잘 엮으면 새로운 지식을 만들 수 있다는 논문이었다.
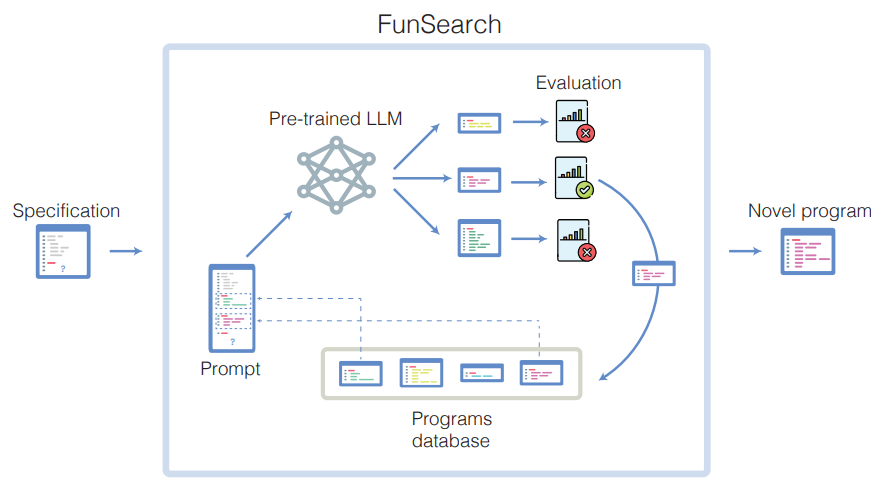
○ 개요 : 새로운 지식을 만드는 함수인 FunSearch (i.e., searching in the function space)를 제시
○ 원리 : evolutionary learning
○ 구성 : LLM은 창의적인 아이디어를 제시하는 요소로 쓰임. evaluator를 넣어서 hallucination (가짜 지식 생성)을 방지
○ 퍼포먼스 : cap set problem 등의 정수론 난제와 online bin packing problem 등의 탐색 알고리즘 문제에 SOTA 해를 제시
2024년 8월에는 가설을 생성하는 end-to-end 논문 쓰는 AI인 The AI Scientist가 발표됐다. 비슷한 맥락으로 곧이어 ADAS가 발표됐다.
입력: 2023.10.07 02:18
수정: 2023.12.17 14:17
'▶ 자연과학 > ▷ 철학' 카테고리의 다른 글
| 【철학】 1강. 지식이란 무엇인가 (4) | 2024.06.02 |
|---|---|
| 【인공지능 철학】 AI는 어디로 가려고 하는가 (0) | 2023.12.05 |
| 【철학】 9강. 정의란 무엇인가 (0) | 2023.03.04 |
| 【명언】 유명한 어구 (0) | 2022.04.02 |
| 【철학】 2강. 과학이란 무엇인가 (0) | 2020.01.03 |



최근댓글